支配树

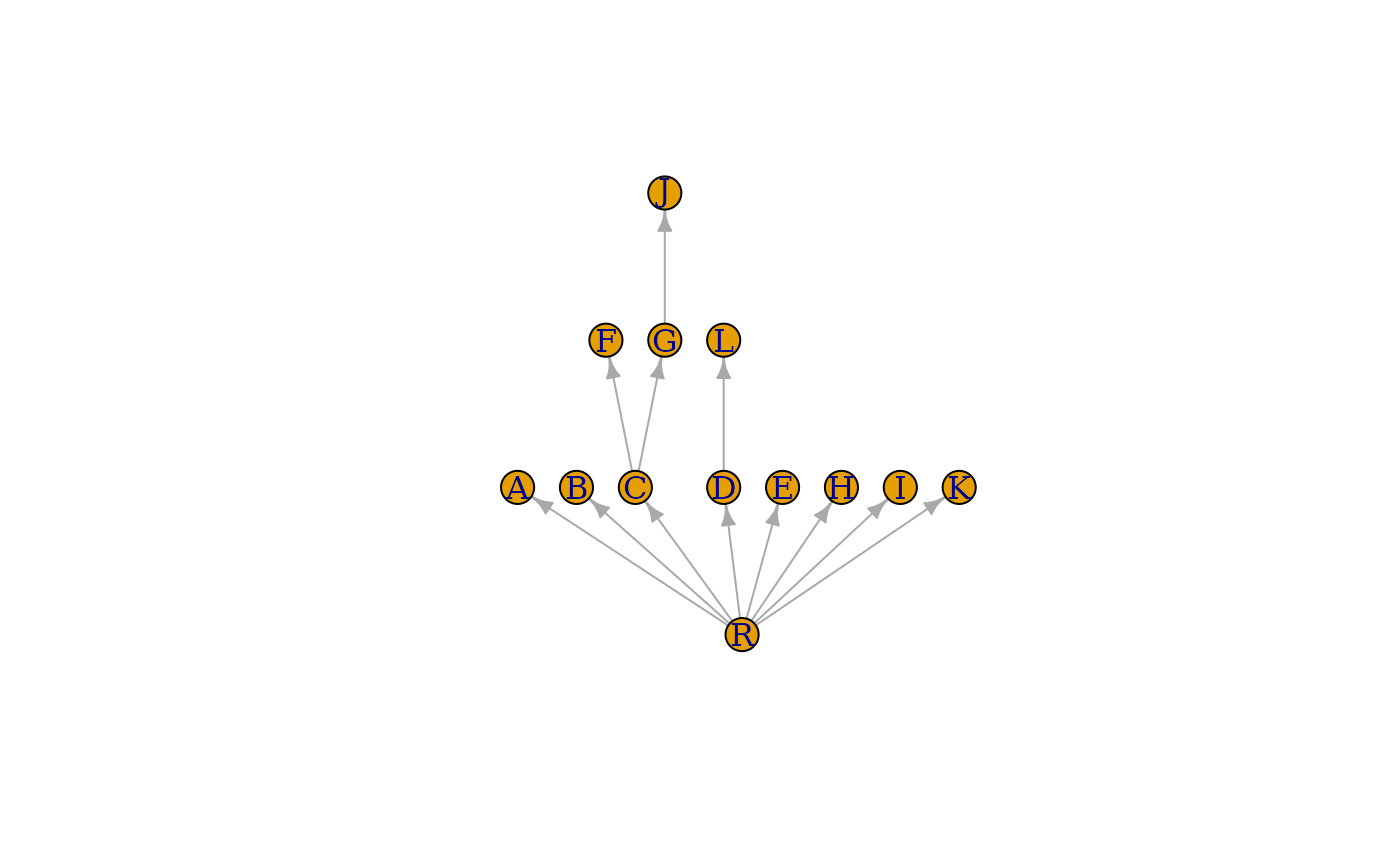
有向图的支配树。

用法

dominator_tree(graph, root, mode = c("out", "in", "all", "total"))

参数

graph

一个有向图。如果它不是一个流图，并且包含一些从根顶点无法到达的顶点，那么这些顶点将被收集并作为结果的一部分返回。

root

根（或源）顶点的 ID，这将是树的根。

mode

常量，必须是 ‘in’ 或 ‘out’。 如果是 ‘in’，那么所有方向都被认为是与输入图中的原始方向相反的。

值

具有以下组件的列表

dom

一个数值向量，给出每个顶点的直接支配者。 对于从根无法到达的顶点，它包含 NaN。 对于根顶点本身，它包含负一。

domtree

一个图对象，支配树。 它的顶点 ID 与输入图的顶点 ID 相同。 孤立顶点是从根无法到达的顶点。

leftout

一个数值向量，包含从根无法到达的顶点 ID。

详细信息

流图是一个具有显著的起始（或根）顶点 \(r\) 的有向图，使得对于任何顶点 \(v\)，都存在一条从 \(r\) 到 \(v\) 的路径。 如果从 \(r\) 到 \(w\) 的每条路径都包含 \(v\)，则顶点 \(v\) 支配另一个顶点 \(w\)（不等于 \(v\)）。 如果 \(v\) 支配 \(w\) 并且 \(w\) 的每个其他支配者都支配 \(v\)，则顶点 \(v\) 是 \(w\) 的直接支配者，\(v=\textrm{idom}(w)\)。 边 \({(\textrm{idom}(w), w)| w \ne r}\) 形成一个有向树，以 \(r\) 为根，称为图的支配树。 当且仅当 \(v\) 是支配树中 \(w\) 的祖先时，顶点 \(v\) 支配顶点 \(w\)。

此函数实现了 Lengauer-Tarjan 算法来构造有向图的支配树。 有关详细信息，请参见下面的参考。

参考文献

Thomas Lengauer, Robert Endre Tarjan: A fast algorithm for finding dominators in a flowgraph, ACM Transactions on Programming Languages and Systems (TOPLAS) I/1, 121–141, 1979.

参见

其他流：edge_connectivity(), is_min_separator(), is_separator(), max_flow(), min_cut(), min_separators(), min_st_separators(), st_cuts(), st_min_cuts(), vertex_connectivity()

作者

Gabor Csardi csardi.gabor@gmail.com

示例

## The example from the paper
g <- graph_from_literal(
  R -+ A:B:C, A -+ D, B -+ A:D:E, C -+ F:G, D -+ L,
  E -+ H, F -+ I, G -+ I:J, H -+ E:K, I -+ K, J -+ I,
  K -+ I:R, L -+ H
)
dtree <- dominator_tree(g, root = "R")
layout <- layout_as_tree(dtree$domtree, root = "R")
layout[, 2] <- -layout[, 2]
plot(dtree$domtree, layout = layout, vertex.label = V(dtree$domtree)$name)