igraph 是一个快速且开源的图或网络分析库。该库的核心是用 C 编写的,并包含高级语言的链接,如 R、Python 和 Mathematica。本教程旨在让你全面了解 igraph 在 R 中的可用功能。有关每个功能的详细信息,请参阅 https://r.igraph.cn/reference/。
注意: 在本教程中,我们将交替使用 图 和 网络,以及 顶点 或 节点。
使用 igraph
要在你的 R 代码中使用 igraph,首先必须加载该库
##
## Attaching package: 'igraph'## The following objects are masked from 'package:stats':
##
## decompose, spectrum## The following object is masked from 'package:base':
##
## union现在你可以使用所有 igraph 功能了。
创建图
igraph 提供了许多创建图的方法。最简单的方法是使用 make_empty_graph() 函数
g <- make_empty_graph()创建图的最常见方法是使用 make_graph(),它基于指定的边构建图。例如,要创建一个具有 10 个节点(编号为 1 到 10)和两个连接节点 1-2 和 1-5 的边的图
g <- make_graph(edges = c(1,2, 1,5), n=10, directed = FALSE)从 igraph 0.8.0 开始,你还可以使用 igraph 公式符号包含文本。在这种情况下,公式的第一项必须以字符 ~ 开头,这在 R 的公式中通常使用。表达式由顶点名称和边运算符组成。边运算符是一系列字符 - 和 +,第一个用于指示实际的边,第二个用于箭头(方向)。你可以使用任意数量的字符 - 来“绘制”它们。如果所有边运算符仅由字符 - 组成,则该图将是非定向的,而单个字符 + 意味着有向图。例如,要创建与之前相同的图
g <- make_graph(~ 1--2, 1--5, 3, 4, 5, 6, 7, 8, 9, 10)我们可以打印该图以获得其节点和边的摘要
g## IGRAPH 20fb2c0 UN-- 10 2 --
## + attr: name (v/c)
## + edges from 20fb2c0 (vertex names):
## [1] 1--2 1--5这意味着:具有 10 个顶点和 2 条边的非定向 (Undirected) 图,这些边在最后一部分中列出。如果该图具有 [名称] 属性,也会打印出来。
注意:summary() 不会列出边,这对于具有数百万条边的大型图来说很方便
summary(g)## IGRAPH 20fb2c0 UN-- 10 2 --
## + attr: name (v/c)此外,make_graph() 可以通过仅指定其名称来创建一些著名的图。例如,你可以生成显示 Zachary 空手道俱乐部社交网络的图,该图反映了 20 世纪 70 年代美国一所大学的 34 名俱乐部成员之间的友谊
g <- make_graph("Zachary")要查看图,你可以使用 plot()
plot(g)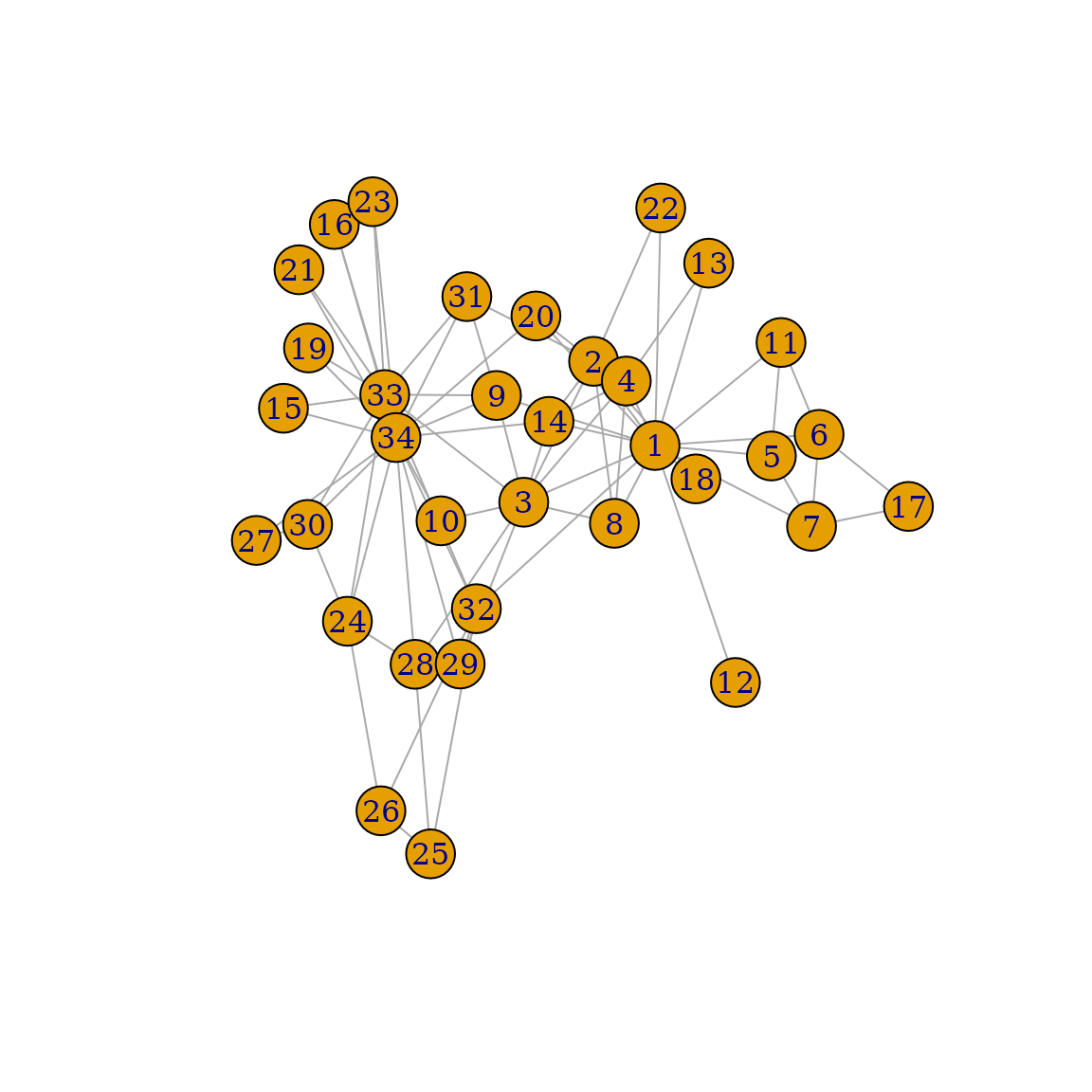
本教程后面提供了有关绘制图的选项的详细说明。
顶点和边 ID
顶点和边在 igraph 中具有数字标识符。顶点 ID 始终是连续的,并且从 1 开始。对于具有“n”个顶点的图,顶点 ID 始终介于 1 和“n”之间。如果任何操作更改图中顶点的数量,例如,通过 induced_subgraph() 创建子图,则会重新枚举顶点以满足此条件。
边也是如此:边 ID 始终介于 1 和“m”之间,即图中的边总数。
注意:如果你熟悉 C 或 igraph 的 Python 接口,你可能已经注意到,在这些语言中,顶点和边 ID 从 0 开始。在 R 接口中,两者都从 1 开始,以与每种语言的约定保持一致。
除了 ID 之外,还可以为顶点和边分配名称和其他属性。这使得在更改图时更容易跟踪它们。本教程后面会展示如何更改这些特征的示例。
添加和删除顶点和边
让我们继续使用空手道俱乐部图。要将一个或多个顶点添加到现有图,请使用 add_vertices()
g <- add_vertices(g, 3)同样,要添加边,你可以使用 add_edges()
通过指定每个边的源顶点 ID 和目标顶点 ID 来添加边。前面的说明添加了三条边,一条连接顶点 1 和 35,另一条连接顶点 1 和 36,还有一条连接顶点 34 和 37。
除了函数 add_vertices() 和 add_edges() 之外,还可以使用“+”运算符将顶点或边添加到图中。执行的操作将取决于右侧的参数类型
你可以使用 add_vertex() 和 add_edge()(单数)一次添加一个顶点/边。
警告:如果需要向图添加多个边,则使用一次 add_edges() 比重复使用 add_edge() 一次添加一个新边效率更高。删除边和顶点也是如此。
如果你尝试将边添加到具有无效 ID 的顶点(例如,你尝试将边添加到顶点 38,而该图只有 37 个顶点),igraph 会显示错误
## Error in add_edges(g, edges = c(38, 37)): At vendor/cigraph/src/graph/type_indexededgelist.c:261 : Out-of-range vertex IDs when adding edges. Invalid vertex ID让我们向我们的图中添加更多顶点和边。在 igraph 中,我们可以使用 magrittr 包,该包提供了一种使用 %>% 运算符链接命令的机制
g <- g %>%
add_edges(edges = c(1, 34)) %>%
add_vertices(3) %>%
add_edges(edges = c(38, 39, 39, 40, 40, 38, 40, 37))
g## IGRAPH 4b0daa9 U--- 40 86 -- Zachary
## + attr: name (g/c)
## + edges from 4b0daa9:
## [1] 1-- 2 1-- 3 1-- 4 1-- 5 1-- 6 1-- 7 1-- 8 1-- 9 1--11 1--12
## [11] 1--13 1--14 1--18 1--20 1--22 1--32 2-- 3 2-- 4 2-- 8 2--14
## [21] 2--18 2--20 2--22 2--31 3-- 4 3-- 8 3--28 3--29 3--33 3--10
## [31] 3-- 9 3--14 4-- 8 4--13 4--14 5-- 7 5--11 6-- 7 6--11 6--17
## [41] 7--17 9--31 9--33 9--34 10--34 14--34 15--33 15--34 16--33 16--34
## [51] 19--33 19--34 20--34 21--33 21--34 23--33 23--34 24--26 24--28 24--33
## [61] 24--34 24--30 25--26 25--28 25--32 26--32 27--30 27--34 28--34 29--32
## [71] 29--34 30--33 30--34 31--33 31--34 32--33 32--34 33--34 1--35 1--36
## + ... omitted several edges现在我们有一个具有 40 个顶点和 89 条边的非定向图。顶点和边 ID 始终是连续的,因此如果删除一个顶点,所有后续顶点都会重新枚举。重新枚举顶点时,不会重新枚举边,但会重新枚举其源顶点和目标顶点。你可以使用 delete_vertices() 和 delete_edges() 执行这些操作。例如,要删除连接顶点 1-34 的边,请获取其 ID,然后删除它
edge_id_para_borrar <- get_edge_ids(g, c(1,34))
edge_id_para_borrar## [1] 82g <- delete_edges(g, edge_id_para_borrar)例如,要创建一个环形图并将其拆分
g <- make_ring(10) %>% delete_edges("10|1")
plot(g)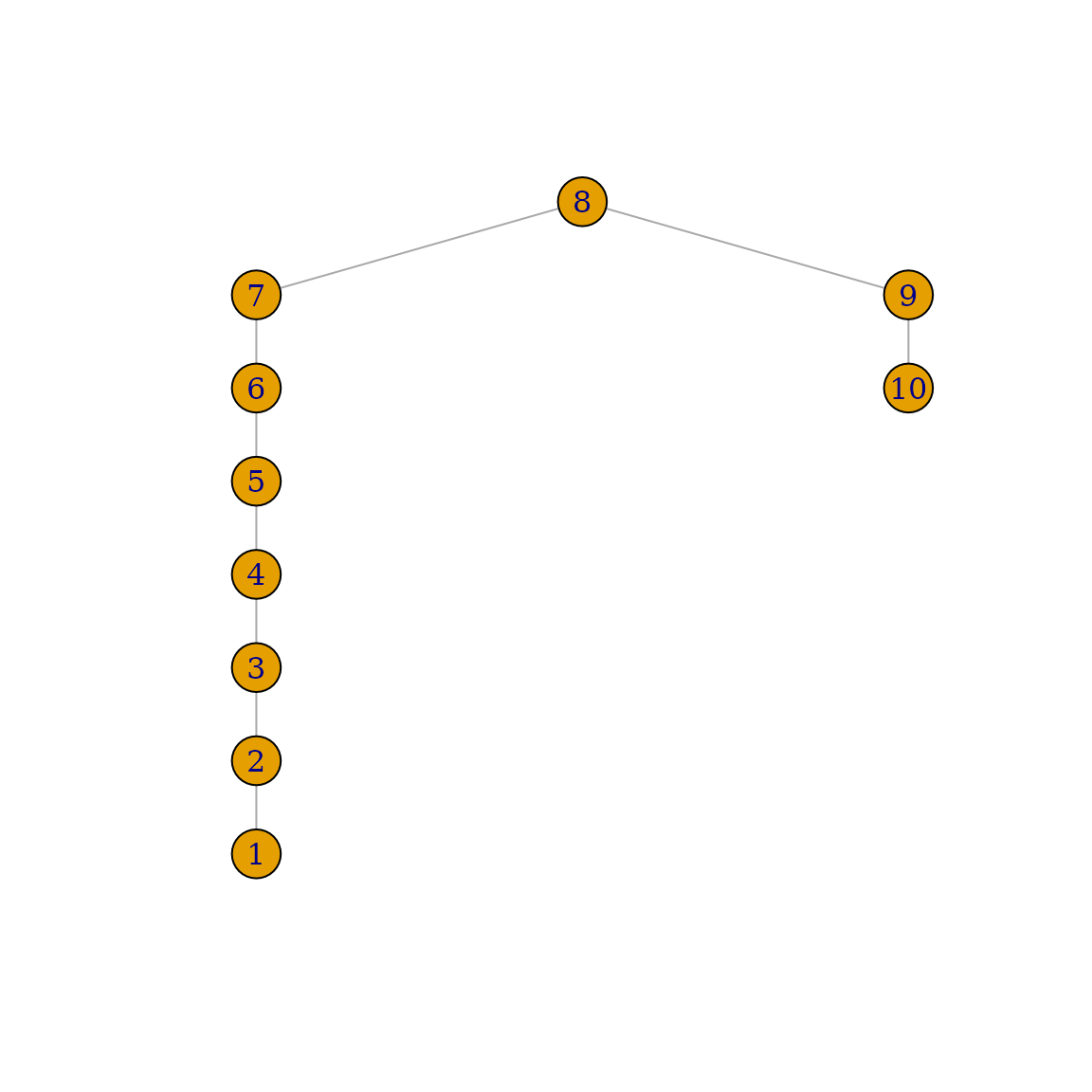
前面的示例表明,你还可以通过指示由符号 | 连接的源顶点和目标顶点的 ID 来引用边。在该示例中,"10|1" 表示连接顶点 10 和顶点 1 的边。当然,你也可以直接使用边 ID,或使用函数 get_edge_ids() 检索它们
g <- make_ring(5)
g <- delete_edges(g, get_edge_ids(g, c(1,5, 4,5)))
plot(g)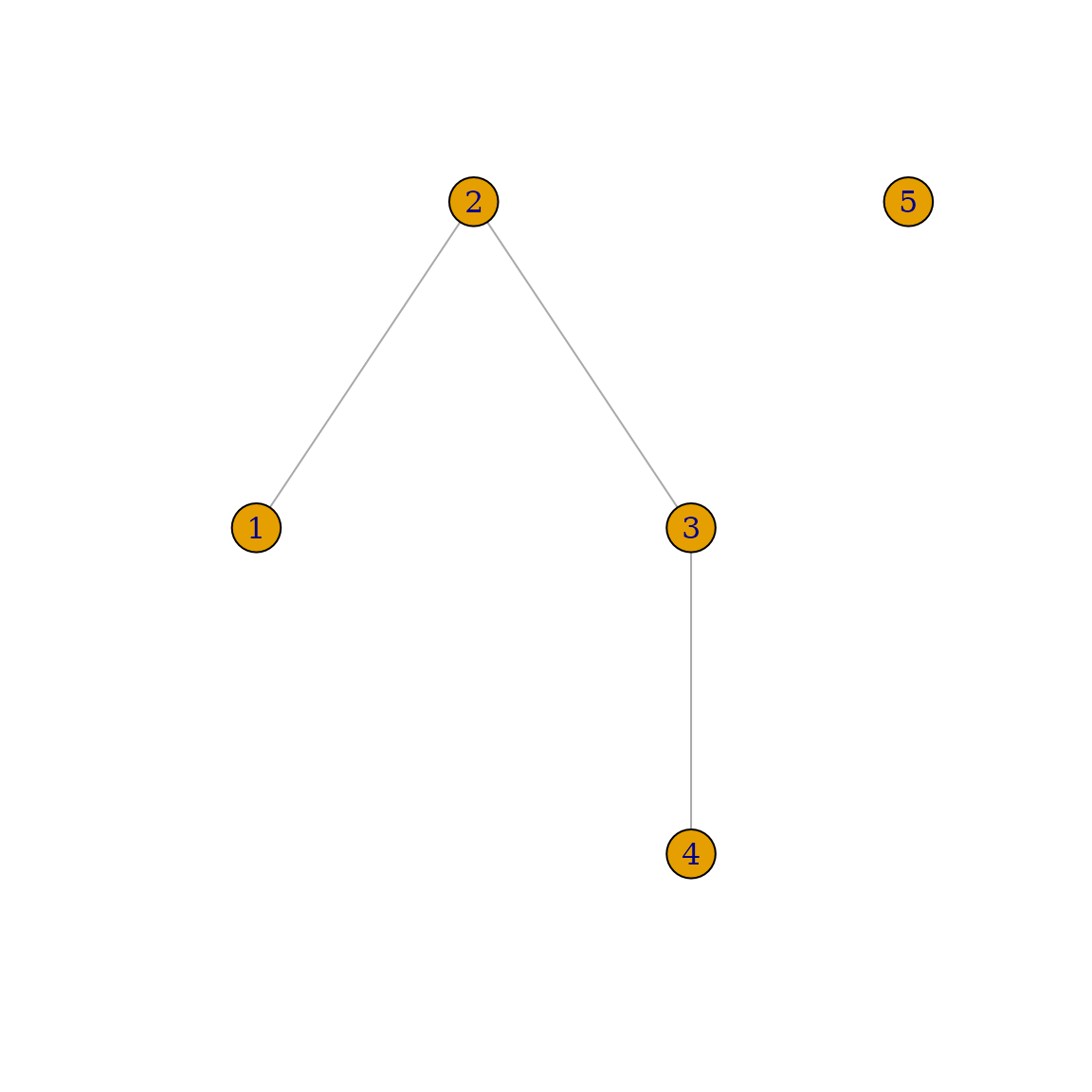
让我们看另一个示例,让我们创建一个弦图。请记住,如果其每个四个或更多节点的循环都有一个“弦”,即连接循环中两个非相邻节点的边,则该图是弦图(或三角图)。首先,让我们使用 graph_from_literal() 创建初始图
g1 <- graph_from_literal(
A-B:C:I,
B-A:C:D,
C-A:B:E:H,
D-B:E:F,
E-C:D:F:H,
F-D:E:G,
G-F:H,
H-C:E:G:I,
I-A:H
)
plot(g1)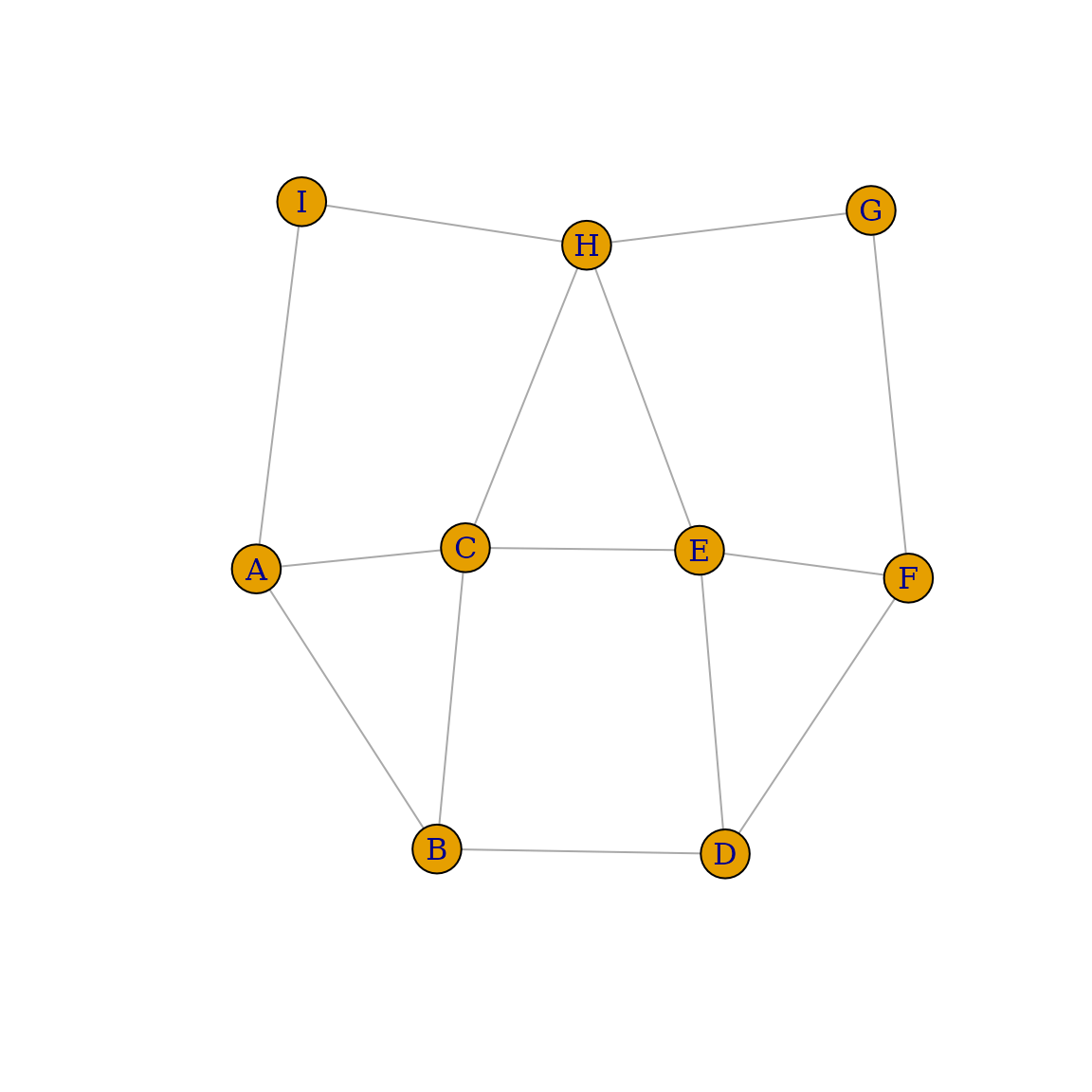
在此示例中,我们使用了运算符 : 来定义顶点集。如果边运算符连接两个顶点集,则第一个集中的每个顶点都将连接到第二个集中的每个顶点。然后,我们使用 is_chordal() 来评估我们的图是否是弦图,并查找填充该图缺少的边
is_chordal(g1, fillin=TRUE)## $chordal
## [1] FALSE
##
## $fillin
## [1] 2 6 8 7 5 7 2 7 6 1 7 1
##
## $newgraph
## NULL然后,在一行中,我们可以添加使初始图成为弦图所需的边
chordal_graph <- add_edges(g1, is_chordal(g1, fillin=TRUE)$fillin)
plot(chordal_graph)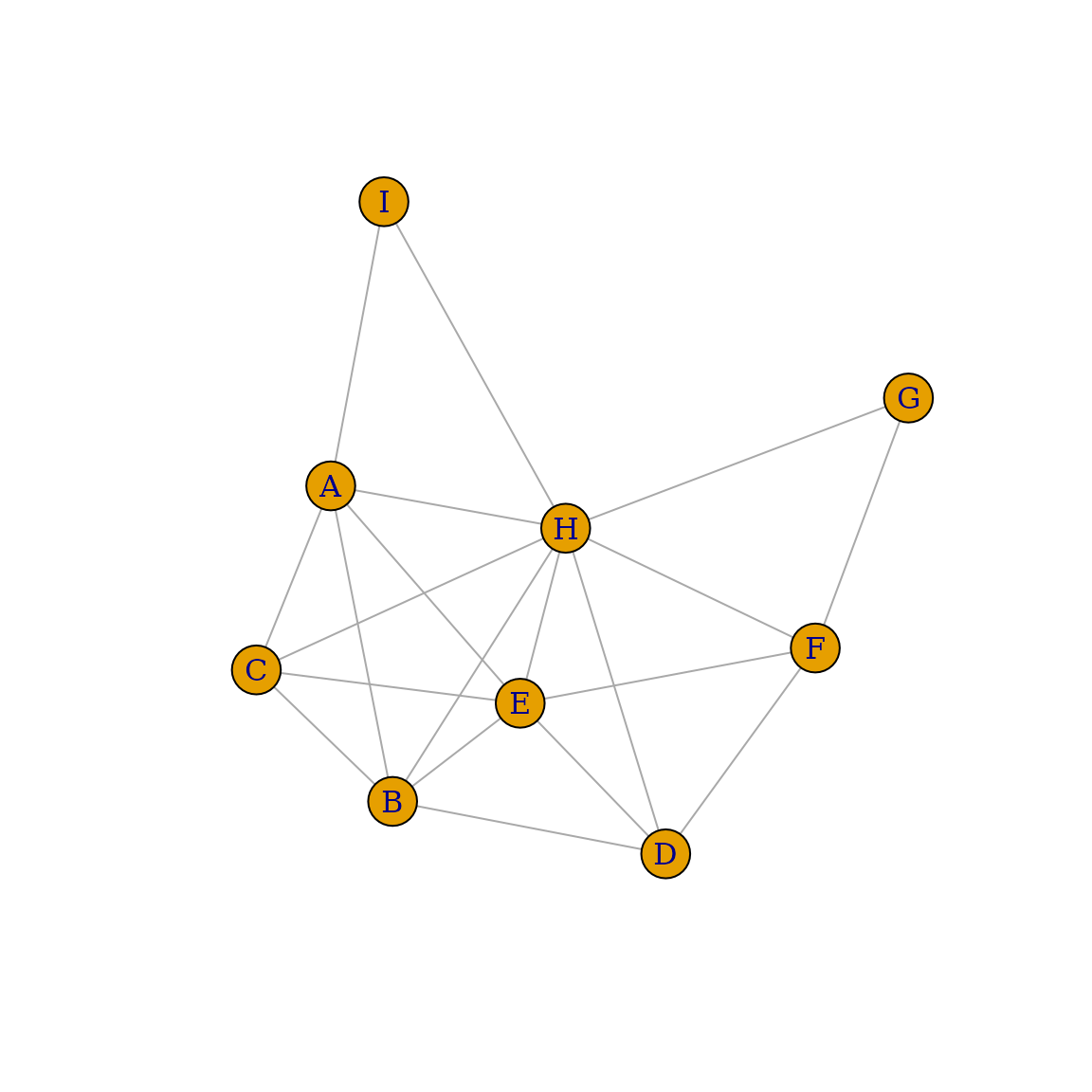
图的构建
除了 make_empty_graph()、make_graph() 和 make_graph_from_literal() 之外,igraph 还包括许多其他用于构建图的函数。有些是确定性的,也就是说,每次都会生成相同的图,例如 make_tree()
## IGRAPH dabaedb U--- 5 3 -- Ring graph
## + attr: name (g/c), mutual (g/l), circular (g/l)这将生成一个具有 127 个顶点的规则树形图,每个顶点都有两个子节点。无论你调用 make_tree() 多少次,如果使用相同的参数,生成的图始终相同
graph2 <- make_tree(127, 2, mode = "undirected")identical_graphs(graph1, graph2)## [1] TRUE其他函数是随机的,这意味着每次都会生成不同的图;例如,sample_grg()
graph1 <- sample_grg(100, 0.2)
summary(graph1)## IGRAPH 6c47506 U--- 100 499 -- Geometric random graph
## + attr: name (g/c), radius (g/n), torus (g/l)这将生成一个随机几何图:在度量空间内随机且均匀地选择 n 个点,并且将彼此最接近的、距离小于预定距离 d 的点对通过边连接。如果使用相同的参数生成 GRG,它们将是不同的
graph2 <- sample_grg(100, 0.2)
identical_graphs(graph1, graph2)## [1] FALSE检查图是否等效的一种稍微宽松的方式是通过 isomorphic()。如果两个图具有相同数量的组件(顶点和边)并且在顶点和边之间保持一对一的对应关系,也就是说,它们以相同的方式连接,则称这两个图是同构的
isomorphic(graph1, graph2)## [1] FALSE对于大型图,检查同构可能需要一段时间(在这种情况下,可以通过检查两个图的度序列来快速给出答案)。identical_graph() 是比 isomorphic() 更严格的标准:两个图必须具有相同的顶点和边列表,且顺序完全相同,具有相同的方向性,并且两个图还必须具有相同的图、顶点和边属性。
设置和检索属性
除了 ID 之外,顶点和边还可以具有属性,例如名称、绘制坐标、元数据和权重。图本身也可以具有这些属性(例如,名称,将显示在 summary 中)。在某种意义上,每个图、顶点和边都可以用作 R 中的命名空间来存储和检索这些属性。
为了演示属性的使用,让我们创建一个简单的社交网络
g <- make_graph(
~ Alice-Boris:Himari:Moshe,
Himari-Alice:Nang:Moshe:Samira,
Ibrahim-Nang:Moshe,
Nang-Samira
)每个顶点代表一个人,因此我们希望存储他们的年龄、性别以及两个人之间的连接类型(is_formal() 指的是一个人与另一个人之间的连接是正式的还是非正式的,即同事或朋友)。运算符 $ 是获取和设置图的属性的快捷方式。它比 graph_attr() 和 set_graph_attr() 更短,也同样可读。
V(g)$age <- c(25, 31, 18, 23, 47, 22, 50)
V(g)$gender <- c("f", "m", "f", "m", "m", "f", "m")
E(g)$is_formal <- c(FALSE, FALSE, TRUE, TRUE, TRUE, FALSE, TRUE, FALSE, FALSE)
summary(g)## IGRAPH 94c0355 UN-- 7 9 --
## + attr: name (v/c), age (v/n), gender (v/c), is_formal (e/l)V 和 E 分别是获取所有顶点和边的序列的标准方法。这会一次为所有顶点/边分配一个属性。生成我们的社交网络的另一种方法是使用 set_vertex_attr() 和 set_edge_attr() 以及运算符 %>%
g <- make_graph(
~ Alice-Boris:Himari:Moshe,
Himari-Alice:Nang:Moshe:Samira,
Ibrahim-Nang:Moshe,
Nang-Samira
) %>%
set_vertex_attr("age", value = c(25, 31, 18, 23, 47, 22, 50)) %>%
set_vertex_attr("gender", value = c("f", "m", "f", "m", "m", "f", "m")) %>%
set_edge_attr("is_formal", value = c(FALSE, FALSE, TRUE, TRUE, TRUE, FALSE, TRUE, FALSE, FALSE))
summary(g)要为单个顶点/边分配或修改属性
E(g)$is_formal## [1] FALSE FALSE TRUE TRUE TRUE FALSE TRUE FALSE FALSE## [1] TRUE FALSE TRUE TRUE TRUE FALSE TRUE FALSE FALSE属性值可以设置为任何 R 对象,但请注意,以某些格式存储图可能会导致复杂属性值丢失。顶点、边和图本身可用于设置属性,例如,向图添加日期
g$date <- c("2022-02-11")
graph_attr(g, "date")## [1] "2022-02-11"要检索属性,你还可以使用 graph_attr()、vertex_attr() 和 edge_attr()。要查找顶点的 ID,你可以使用函数 match()
## [1] 7要将属性分配给顶点或边的子集,你可以使用
## + 7/7 vertices, named, from 94c0355:
## [1] Alejandra Bruno Carmina Moshe Nang Samira Ibrahim要删除属性
g <- delete_vertex_attr(g, "gender")
V(g)$gender## NULL图的结构属性
igraph 提供了一组广泛的方法来计算图的各种结构属性。记录所有这些方法超出了本教程的范围,因此本节仅出于说明目的介绍其中一些方法。我们将使用我们在上一节中构建的小型社交网络。
你可能想到的最简单的属性可能是“顶点度”。顶点的度等于与其关联的边的数量。对于有向图,我们还可以定义入度(指向顶点的边的数量)和出度(从顶点发出的边的数量)。 igraph 能够使用简单的语法计算所有这些
degree(g)## Alejandra Bruno Carmina Moshe Nang Samira Ibrahim
## 3 1 4 3 3 2 2如果图是有向图,我们可以使用 degree(mode = "in") 和 degree(mode = "out") 分别计算入度和出度。如果只想计算顶点子集的度,你还可以将单个顶点 ID 或顶点 ID 列表传递给 degree()
degree(g, 7)## Ibrahim
## 2## Carmina Moshe Nang
## 4 3 3大多数接受顶点 ID 的函数也接受顶点“名称”(即顶点 name 属性的值),前提是名称是唯一的
## Carmina Moshe Nang
## 4 3 3它也适用于单个顶点
degree(g, "Bruno")## Bruno
## 1同样,对于 igraph 可以计算的大多数结构属性,都使用类似的语法。对于顶点属性,函数接受 ID、名称或 ID 或名称列表(如果省略,则默认为所有顶点的集合)。对于边属性,函数接受单个 ID 或 ID 列表。
注意: 对于某些度量,仅计算少量顶点或边而不是整个图没有意义,因为无论如何都需要花费相同的时间。在这种情况下,函数不接受顶点或边 ID,但你可以使用标准操作限制结果列表。一个示例是特征向量中心性 (evcent())。
除了度数之外,igraph 还包括用于计算许多其他中心性属性的内置函数,例如顶点和边介数中心性 (edge_betweenness()) 或 Google PageRank (page_rank()),仅举几例。在这里,我们仅说明边介数中心性
## [1] 6 6 4 3 4 4 4 2 3这样,我们现在还可以找出哪些连接具有最高的介数中心性
ebs <- edge_betweenness(g)
as_edgelist(g)[ebs == max(ebs), ]## [,1] [,2]
## [1,] "Alejandra" "Bruno"
## [2,] "Alejandra" "Carmina"基于属性搜索顶点和边
选择顶点
以先前创建的社交网络为例,你想找出谁的度数最高。你可以使用到目前为止介绍的工具和函数 which.max() 来执行此操作
## Carmina
## 3另一个示例是仅选择具有奇数 ID 的顶点,使用函数 V()
graph <- graph.full(n=10)## Warning: `graph.full()` was deprecated in igraph 2.1.0.
## ℹ Please use `make_full_graph()` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.## [1] 5当然,可以使用位置索引选择顶点或边
seq <- V(graph)[2, 3, 7]
seq## + 3/10 vertices, from b4b875e:
## [1] 2 3 7seq <- seq[1, 3] # filtrar un conjunto de vértices existente
seq## + 2/10 vertices, from b4b875e:
## [1] 2 7选择不存在的顶点会生成错误
seq <- V(graph)[2, 3, 7, "foo", 3.5]## Error in `simple_vs_index()` at rigraph/R/iterators.R:736:7:
## ! Unknown vertex selected.属性名称也可以按原样在 V() 和 E() 的索引运算符(“[]”)中使用。这可以与 R 使用布尔向量进行索引的能力相结合,以获得非常简洁且可读的表达式,用于检索图中顶点或边的子集。例如,以下命令为我们提供了社交网络中小于 30 岁的人的姓名
V(g)[age < 30]$name## [1] "Alejandra" "Carmina" "Moshe" "Samira"当然,< 不是唯一可以使用的布尔运算符。其他可能性如下
| 运算符 | 含义 |
|---|---|
== |
属性/属性的值必须等于 |
!= |
属性/属性的值必须不等于 |
< |
属性/属性的值必须小于 |
<= |
属性/属性的值必须小于或等于 |
> |
属性/属性的值必须大于 |
>= |
属性/属性的值必须大于或等于 |
%in% |
属性/属性的值必须包含在 |
你还可以使用 Negate 运算符从 %in% 创建一个“未包含在”运算符
`%notin%` <- Negate(`%in%`)如果一个属性与 igraph 的函数具有相同的名称,你必须小心,因为语法可能会变得有点混乱。例如,如果有一个名为 degree 的属性表示每个人的考试成绩,则不应将其与计算网络中顶点度的 igraph 函数混淆
## [1] "A" "A+" "C"## [1] "Alejandra" "Moshe" "Nang"选择边
可以基于属性选择边,就像选择顶点一样。如前所述,获取边的标准方法是 E。此外,还有一些用于选择边的特殊结构属性。
使用 .from() 允许从边的来源顶点过滤边序列。例如,选择来自 Carmina(其顶点 ID 为 3)的所有边
## + 4/9 edges from 94c0355 (vertex names):
## [1] Alejandra--Carmina Carmina --Moshe Carmina --Nang Carmina --Samira当然,它也适用于顶点名称
## + 4/9 edges from 94c0355 (vertex names):
## [1] Alejandra--Carmina Carmina --Moshe Carmina --Nang Carmina --Samira通过使用 .to(),根据目标或目标顶点过滤边序列。如果图是有向图,则这与 .from() 不同,而对于无向图,则会给出相同的答案。使用 .inc() 仅选择在一个或至少一个顶点上发生的边,而不管边的方向如何。
表达式 %--% 是一个特殊运算符,可用于选择两个顶点集之间的所有边。它忽略有向图中边的方向。例如,以下表达式选择 Carmina(其顶点 ID 为 3)、Nang(其顶点 ID 为 5)和 Samira(其顶点 ID 为 6)之间的所有边
## + 3/9 edges from 94c0355 (vertex names):
## [1] Carmina--Nang Carmina--Samira Nang --Samira为了使运算符 %--% 与名称一起使用,你可以构建包含名称的字符向量,然后使用这些向量作为操作数。例如,要选择所有连接男性和女性的边,我们可以执行以下操作,然后在我们先前删除后重新添加性别属性
men <- V(g)[gender == "m"]$name
men## [1] "Bruno" "Moshe" "Nang" "Ibrahim"women <- V(g)[gender == "f"]$name
women## [1] "Alejandra" "Carmina" "Samira"## + 5/9 edges from 94c0355 (vertex names):
## [1] Alejandra--Bruno Alejandra--Moshe Carmina --Moshe Carmina --Nang
## [5] Nang --Samira将图视为邻接矩阵
邻接矩阵是表示图的另一种方式。在邻接矩阵中,行和列由图的顶点指示,矩阵元素指示顶点 i 和 j 之间的边数。我们的虚构社交网络的图的邻接矩阵为
## 7 x 7 sparse Matrix of class "dgCMatrix"
## Alejandra Bruno Carmina Moshe Nang Samira Ibrahim
## Alejandra . 1 1 1 . . .
## Bruno 1 . . . . . .
## Carmina 1 . . 1 1 1 .
## Moshe 1 . 1 . . . 1
## Nang . . 1 . . 1 1
## Samira . . 1 . 1 . .
## Ibrahim . . . 1 1 . .例如,Carmina (1, 0, 0, 1, 1, 1, 0) 直接连接到 Alejandra(其索引为 1)、Moshe(索引 4)、Nang(索引 5)、Samira(索引 6)和,但不连接到 Bruno(索引 2)或 Ibrahim(索引 7)。
布局和绘图
图是一个抽象数学对象,在 2D、3D 或任何几何空间中没有特定的表示形式。这意味着,当我们想要可视化图时,我们首先必须在顶点和二维或三维空间中的坐标之间找到对应关系,最好以一种有用和/或令人赏心悦目的方式。图论的一个单独分支,称为图绘制,致力于通过各种图布局算法解决此问题。 igraph 实现了多个布局算法,并且还能够将其绘制在屏幕上或 R 本身支持的任何输出格式中。
布局算法
igraph 中的布局函数始终以 layout 开头。下表总结了它们
| 方法名称 | 算法说明 |
|---|---|
layout_randomly |
完全随机地放置顶点 |
layout_in_circle |
确定性布局,将顶点放置在圆圈中 |
layout_on_sphere |
确定性布局,将顶点均匀地放置在球体表面上 |
layout_with_drl |
用于大型图的 DRL(分布式递归布局)算法 |
layout_with_fr |
有向 Fruchterman-Reingold 算法 |
layout_with_kk |
有向 Kamada-Kawai 算法 |
layout_with_lgl |
用于大型图的 LGL(大型图布局)算法 |
layout_as_tree |
Reingold-Tilford 树布局,适用于(几乎)树状图 |
layout_nicely |
布局算法,根据图的某些属性自动选择其他算法之一 |
可以使用图作为第一个参数直接运行布局算法。它们将返回一个矩阵,其中包含两列,行数与图中的顶点数相同;每一行对应于单个顶点的位置,按顶点 ID 排序。某些算法具有 3D 变体;在这种情况下,它们返回三列而不是 2 列。
layout <- layout_with_kk(g)某些布局算法采用其他参数;例如,当以树的形式布局图时,指定哪个顶点应放置在布局的根目录中可能是有意义的
layout <- layout_as_tree(g, root = 2)使用布局绘制图
我们可以使用 Kamada-Kawai 布局算法绘制我们的虚构社交网络,如下所示
layout <- layout_with_kk(g)plot(g, layout = layout, main = "Red social con el algoritmo de diseño Kamada-Kawai")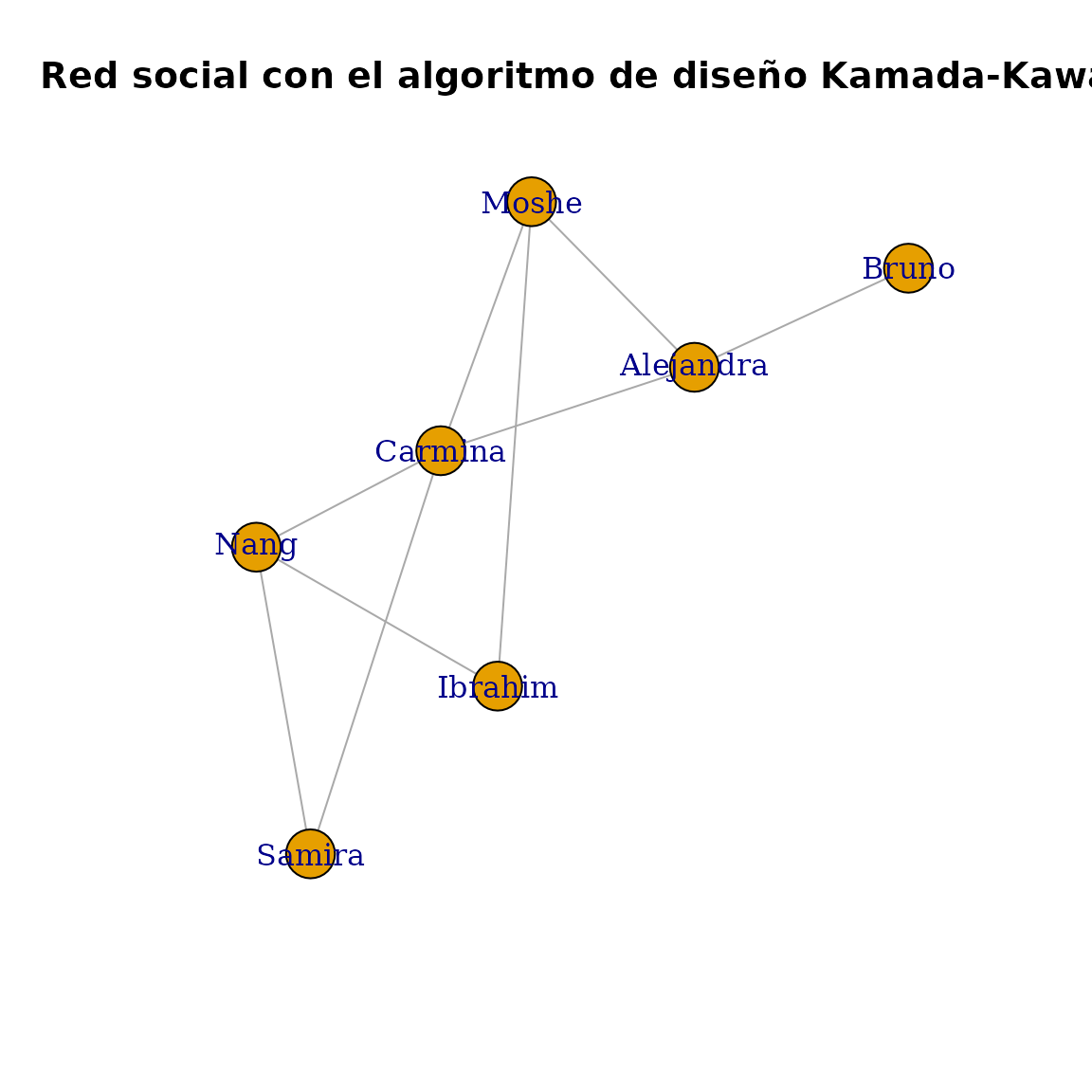
这应该会打开一个新窗口,显示网络的视觉表示。请记住,节点的确切位置在你的机器上可能有所不同,因为布局不是确定性的。
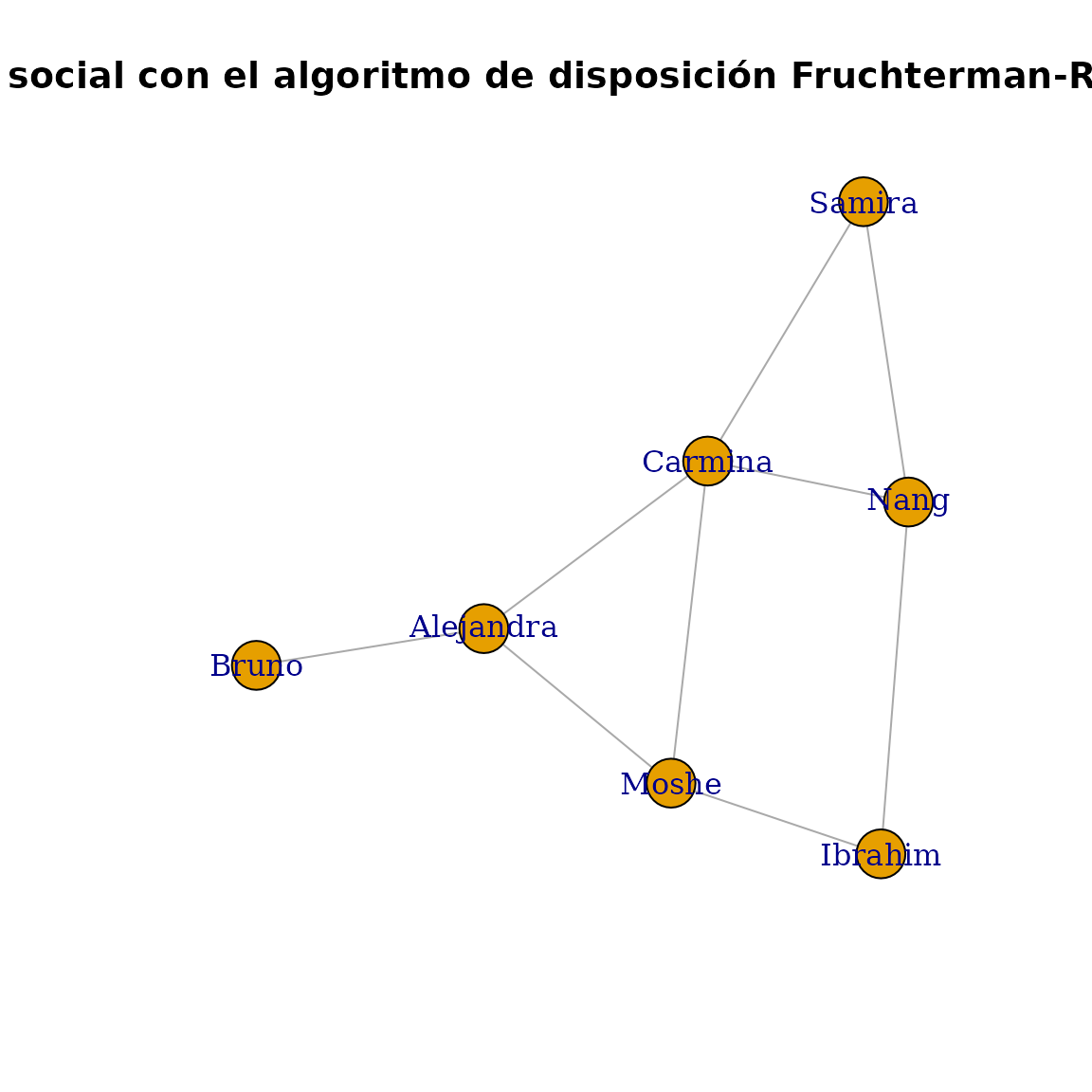
参数 layout 也接受函数;在这种情况下,将使用图作为其第一个参数调用该函数。这允许直接输入布局函数的名称,而无需像前面的示例中那样创建布局变量
plot(
g,
layout = layout_with_fr,
main = "Red social con el algoritmo de disposición Fruchterman-Reingold"
)
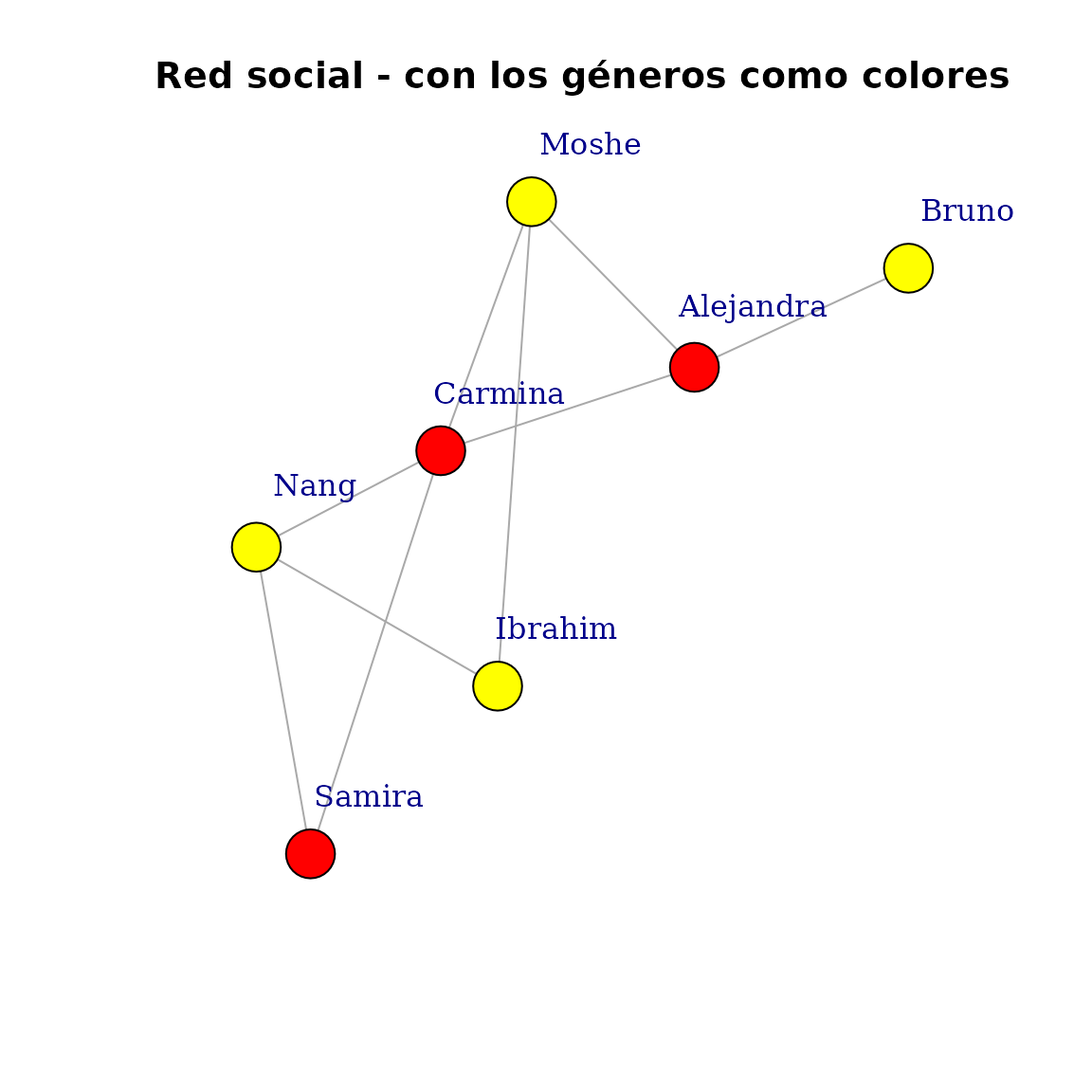
为了改善视觉外观,一个简单的补充是根据性别对顶点进行着色。我们还应该尝试将名称放置在顶点之外一点,以提高可读性
V(g)$color <- ifelse(V(g)$gender == "m", "yellow", "red")
plot(
g,
layout = layout,
vertex.label.dist = 3.5,
main = "Red social - con los géneros como colores"
)
你还可以将属性 gender 视为一个因子,并将颜色作为参数提供给 plot(),它优先于标准分配给顶点的属性 color。颜色会自动分配
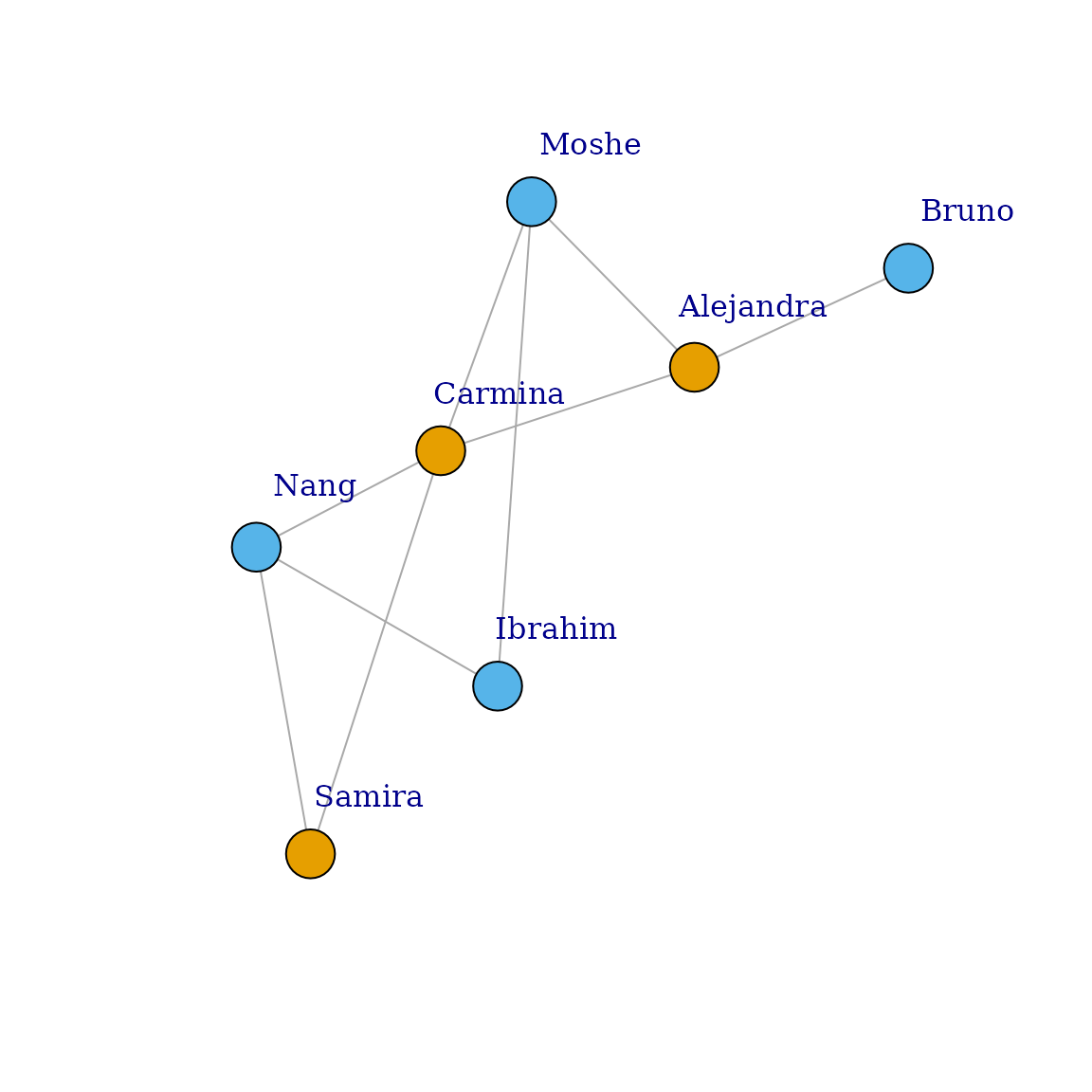
如前所述,使用参数 vertex.color,你可以为 plot 指定视觉属性,而不是使用和/或操作顶点或边属性。下图显示了带有粗线的正式关系和带有细线的非正式关系
plot(
g,
layout = layout,
vertex.label.dist = 3.5,
vertex.size = 20,
vertex.color = ifelse(V(g)$gender == "m", "yellow", "red"),
edge.width = ifelse(E(g)$is_formal, 5, 1)
)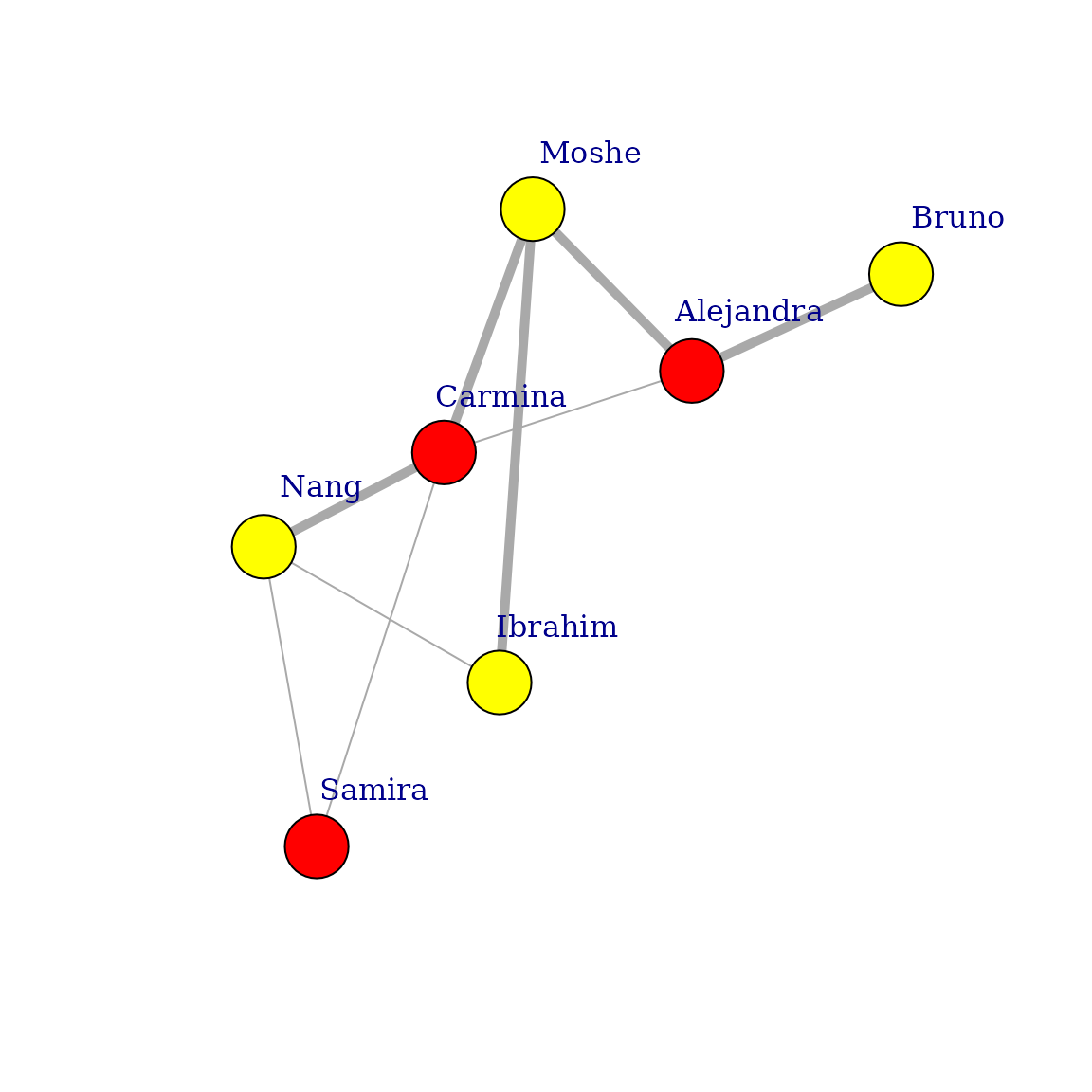
如果要修改图的视觉表示形式,但不希望对图本身进行修改,则首选此最新过程。
总而言之,顶点和边有一些特殊属性,对应于图的视觉表示形式。这些属性可以修改 igraph 的默认设置(即颜色、权重、名称、形状、布局等)。下表分别总结了顶点和边最常用的视觉属性
用于绘图的顶点属性
| 属性名称 | 参数 | 目的 |
|---|---|---|
颜色 |
vertex.color |
顶点颜色 |
标签 |
vertex.label |
顶点标签。它们将被转换为字符。指定 NA 以省略顶点标签。默认顶点标签是顶点 ID。 |
label.cex |
vertex.label.cex |
顶点标签的字体大小,被解释为一个乘法因子,类似于 R 的 text 函数 |
label.color |
vertex.label.color |
顶点标签颜色 |
label.degree |
vertex.label.degree |
定义顶点标签相对于其中心的放置位置。它被解释为弧度角,零表示“右侧”,’pi’ 表示左侧,上方为 -pi/2,下方为 pi/2。默认值为 -pi/4 |
label.dist |
vertex.label.dist |
顶点标签与顶点本身的距离,相对于顶点的大小 |
label.family |
vertex.label.family |
顶点字体系列,类似于 R 的 text 函数 |
label.font |
vertex.label.font |
顶点字体系列中的字体,类似于 R 的 text 函数 |
形状 |
vertex.shape |
顶点形状,目前支持“circle”、“square”、“csquare”、“rectangle”、“crectangle”、“vrectangle”、“pie”(请参阅 vertex.shape.pie)、‘sphere’ 和“none”,并且仅由命令 plot.igraph 支持 |
大小 |
vertex.size |
顶点大小,一个数值标量或向量,在后一种情况下,每个顶点的大小可能不同 |
用于绘图的边属性
| 属性名称 | 参数 | 目的 |
|---|---|---|
颜色 |
edge.color |
边颜色 |
curved |
edge.curved |
数值指定边的曲率;零曲率表示直线边,负值表示边按顺时针方向弯曲,正值表示相反的方向。 TRUE 表示曲率 0.5,FALSE 表示零曲率 |
arrow.size |
edge.arrow.size |
当前是一个常量,因此对于所有边都是相同的。如果存在一个向量,则仅使用第一个元素,也就是说,如果从边属性获取,则仅使用第一个边的属性用于所有箭头 |
arrow.width |
edge.arrow.width |
箭头的宽度。当前是一个常量,因此对于所有边都是相同的 |
width |
edge.width |
边的宽度(以像素为单位) |
标签 |
edge.label |
如果指定,将标签添加到边 |
label.cex |
edge.label.cex |
边标签的字体大小,被解释为一个乘法因子,类似于 R 的 text 函数 |
label.color |
edge.label.color |
边标签颜色 |
label.family |
edge.label.family |
边字体系列,类似于 R 的 text 函数 |
label.font |
edge.label.font |
边字体系列中的字体,类似于 R 的 text 函数 |
igraph 与外部世界
如果没有某种导入/导出功能,允许包与外部程序和工具包进行通信,那么任何图模块都将是不完整的。 igraph 也不例外:它提供了读取最常见的图格式以及将图保存到符合这些格式规范的文件中的函数。用于从文件读取和写入文件的主要函数分别是 read_graph() 和 write_graph()。下表总结了 igraph 可以读取或写入的格式
| 格式 | 简称 | 读取方法 | 写入方法 |
|---|---|---|---|
| 邻接表(又名 LGL) | lgl |
read_graph(file, format = c("lgl")) |
write_graph(graph, file, format = c("lgl")) |
| 邻接矩阵 | adjacency |
graph_from_adjacency_matrix(adjmatrix, mode = c("directed", "undirected", "max", "min", "upper","lower", "plus"), weighted = NULL, diag = TRUE, add.colnames = NULL, add.rownames = NA) |
as.matrix(graph, "adjacency") |
| DIMACS | dimacs |
read_graph(file, format = c("dimacs")) |
write_graph(graph, file, format = c("dimacs")) |
| 边列表 | edgelist |
read_graph(file, format = c("edgelist")) |
write_graph(graph, file, format = c("edgelist")) |
| GraphViz | dot |
尚不支持 | write_graph(graph, file, format = c("dot")) |
| GML | gml |
read_graph(file, format = c("gml")) |
write_graph(graph, file, format = c("gml")) |
| GraphML | graphml |
read_graph(file, format = c("graphml")) |
write_graph(graph, file, format = c("graphml")) |
| LEDA | leda |
尚不支持 | write_graph(graph, file, format = c("leda")) |
| 带标签的边列表(又名 NCOL) | ncol |
read_graph(file, format = c("ncol")) |
write_graph(graph, file, format = c("ncol")) |
| Pajek 格式 | pajek |
read_graph(file, format = c("pajek")) |
write_graph(graph, file, format = c("pajek")) |
注意: 大多数格式都有其自身的限制;例如,并非所有格式都可以存储属性。如果你想将igraph的图保存为可以从外部包读取的格式,并且希望保留数字和字符串属性,那么GraphML或GML可能是你最好的选择。边列表 和 NCOL 也不错,如果你没有属性(尽管 NCOL 支持顶点名称和边权重)。
下一步去哪里
本教程是对R语言中 igraph 的简要介绍。我们希望你喜欢阅读它,并且发现它对你自己的网络分析有用。
有关特定功能的详细描述,请参阅 https://r.igraph.cn/reference/。如果您有关于如何使用 igraph 的问题,请访问我们的 论坛。要报告错误,请在 Github 上打开一个 问题。请不要直接在 Github 上提出使用问题,因为它面向开发者而不是用户。
会话信息
为了可重现性,上述代码的会话信息如下
## R version 4.5.1 (2025-06-13)
## Platform: x86_64-pc-linux-gnu
## Running under: Ubuntu 24.04.2 LTS
##
## Matrix products: default
## BLAS: /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3
## LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so; LAPACK version 3.12.0
##
## locale:
## [1] LC_CTYPE=C.UTF-8 LC_NUMERIC=C LC_TIME=C.UTF-8
## [4] LC_COLLATE=C.UTF-8 LC_MONETARY=C.UTF-8 LC_MESSAGES=C.UTF-8
## [7] LC_PAPER=C.UTF-8 LC_NAME=C LC_ADDRESS=C
## [10] LC_TELEPHONE=C LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C
##
## time zone: UTC
## tzcode source: system (glibc)
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] igraph_2.1.4.9069
##
## loaded via a namespace (and not attached):
## [1] crayon_1.5.3 vctrs_0.6.5 cli_3.6.5 knitr_1.50
## [5] rlang_1.1.6 xfun_0.52 textshaping_1.0.1 jsonlite_2.0.0
## [9] glue_1.8.0 htmltools_0.5.8.1 ragg_1.4.0 sass_0.4.10
## [13] rmarkdown_2.29 grid_4.5.1 evaluate_1.0.4 jquerylib_0.1.4
## [17] fastmap_1.2.0 yaml_2.3.10 lifecycle_1.0.4 compiler_4.5.1
## [21] fs_1.6.6 htmlwidgets_1.6.4 pkgconfig_2.0.3 lattice_0.22-7
## [25] systemfonts_1.2.3 digest_0.6.37 R6_2.6.1 pillar_1.11.0
## [29] magrittr_2.0.3 Matrix_1.7-3 bslib_0.9.0 tools_4.5.1
## [33] pkgdown_2.1.3.9000 cachem_1.1.0 desc_1.4.3