跳到内容

图上的 SIR 模型

来源：R/epi.R，R/sir.R
sir.Rd

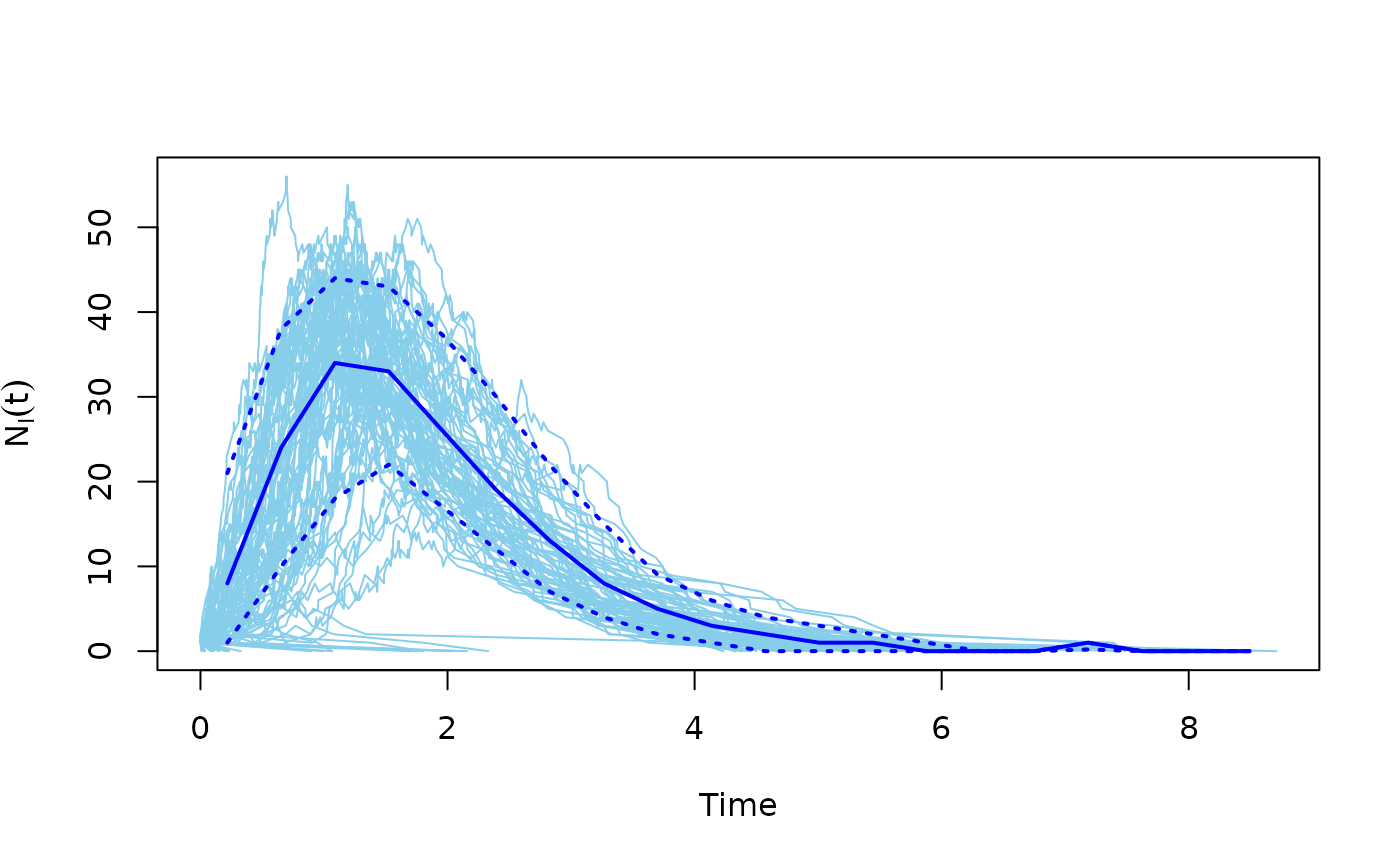
在图上运行 SIR（易感-感染-恢复）模型的模拟

用法

time_bins(x, middle = TRUE)

# S3 method for class 'sir'
time_bins(x, middle = TRUE)

# S3 method for class 'sir'
median(x, na.rm = FALSE, ...)

# S3 method for class 'sir'
quantile(x, comp = c("NI", "NS", "NR"), prob, ...)

sir(graph, beta, gamma, no.sim = 100)

参数

x

由 sir() 函数返回的 sir 对象。

middle

逻辑标量，表示是返回时间箱的中间值还是边界值。

na.rm

逻辑标量，表示是否忽略 NA 值。 sir 对象当前不包含任何 NA 值，因此此参数实际上被忽略。

...

附加参数，目前被忽略。

comp

字符标量。要计算分位数的组件。NI 是受感染的个体，NS 是易感个体，NR 代表已恢复个体。

prob

概率的数值向量，在 [0,1] 中，它们指定要计算的分位数。

graph

要在其上运行模型的图。如果是有向图，则忽略边的方向并给出警告。

beta

非负标量。易感个体且只有一个受感染邻居的感染率。具有 n 个受感染邻居的易感个体的感染率是 beta 的 n 倍。形式上，这是指数分布的速率参数。

gamma

正标量。受感染个体的恢复率。形式上，这是指数分布的速率参数。

no.sim

整数标量，要执行的模拟运行次数。

值

对于 sir()，结果以 ‘sir’ 类的对象返回，这是一个列表，每个模拟运行一个元素。每个模拟本身都是一个列表，包含以下元素。它们都是数值向量，长度相等

times

事件的时间。

NS

人口中易感个体的数量，随时间变化。

NI

人口中受感染个体的数量，随时间变化。

NR

人口中已恢复个体的数量，随时间变化。

函数 time_bins() 返回一个数值向量，表示时间箱的中间值或边界值，具体取决于 middle 参数。

median 返回一个包含三个命名数值向量的列表，分别是 NS、NI 和 NR。向量中的名称由时间箱创建。

如果仅请求一个分位数，则 quantile 返回与 median 相同的向量（但仅返回一个请求的向量）。如果请求多个分位数，则返回这些向量的列表，每个分位数一个。

详细信息

SIR 模型是流行病学中的一个简单模型。人口中的个体可能处于三种状态：易感、感染和恢复。恢复的人被认为是对此疾病免疫的。易感个体以取决于其受感染邻居数量的速率被感染。受感染的人以恒定速率恢复。

函数 sir() 模拟该模型。此函数运行多个模拟，所有模拟都从单个均匀随机选择的受感染个体开始。当没有受感染的个体时，模拟停止。

函数 time_bins() 使用 Freedman-Diaconis 启发式方法对模拟步骤进行分箱，以确定箱宽度。

函数 median 和 quantile 分别计算结果的中位数和分位数，并使用 time_bins() 计算箱。

参考文献

Bailey, Norman T. J. (1975). 传染病的数学理论及其应用（第 2 版）。伦敦：Griffin。

参见

plot.sir() 用于方便地绘制结果

图上的过程 plot.sir()

作者

Gabor Csardi csardi.gabor@gmail.com。Eric Kolaczyk (http://math.bu.edu/people/kolaczyk/) 在 R 中编写了初始版本。

sir().

示例


g <- sample_gnm(100, 100)
sm <- sir(g, beta = 5, gamma = 1)
plot(sm)