跳到内容

计算内聚块

来源：R/cohesive.blocks.R
cohesive_blocks.Rd

为 igraph 类的对象计算内聚块。

用法

cohesive_blocks(graph, labels = TRUE)

# S3 method for class 'cohesiveBlocks'
length(x)

blocks(blocks)

graphs_from_cohesive_blocks(blocks, graph)

# S3 method for class 'cohesiveBlocks'
cohesion(x, ...)

hierarchy(blocks)

parent(blocks)

# S3 method for class 'cohesiveBlocks'
print(x, ...)

# S3 method for class 'cohesiveBlocks'
summary(object, ...)

# S3 method for class 'cohesiveBlocks'
plot(
  x,
  y,
  colbar = rainbow(max(cohesion(x)) + 1),
  col = colbar[max_cohesion(x) + 1],
  mark.groups = blocks(x)[-1],
  ...
)

plot_hierarchy(
  blocks,
  layout = layout_as_tree(hierarchy(blocks), root = 1),
  ...
)

export_pajek(blocks, graph, file, project.file = TRUE)

max_cohesion(blocks)

参数

graph

对于 cohesive_blocks()，是一个 igraph 类的图对象。它必须是无向的和简单的。（参见 is_simple()。）

对于 graphs_from_cohesive_blocks() 和 export_pajek()，必须提供相同的图，其内聚块结构在 blocks() 参数中给出。

labels

逻辑标量，是否将顶点标签添加到结果对象。这些标签可以在报告和绘制内聚块时使用。

blocks, x, object

一个 cohesiveBlocks 对象，使用 cohesive_blocks() 函数创建。

...

附加参数。plot_hierarchy() 和 plot() 将它们传递给 plot.igraph()。print() 和 summary() 忽略它们。

y

图，其内聚块在 x 参数中提供。

colbar

顶点颜色的颜色条。其长度应至少为 \(m+1\)，其中 \(m\) 是图中最大的内聚度。或者，也可以通过 col 参数直接指定顶点颜色。

col

顶点颜色的向量，以任何常用格式。（符号颜色名称（例如“red”、“blue”等），RGB 颜色（例如“#FF9900FF”），引用当前调色板的整数。默认情况下，使用给定的 colbar，并且具有相同最大内聚度的顶点将具有相同的颜色。

mark.groups

要在图中标记的顶点集合列表，通过用圆圈圈起来。默认情况下，标记所有内聚块，除了对应于所有顶点的那个。

layout

绘图的布局，它只是传递给 plot.igraph()，参见那里的可能格式。默认情况下，使用 Reingold-Tilford 布局生成器。

file

定义 Pajek 文件写入的文件（或连接）。

如果 project.file 参数为 TRUE，则它可以是文件名（带扩展名）、文件对象，或者通常是任何类型的连接对象。如果文件/连接尚未打开，则会将其打开。

如果 project.file 参数为 FALSE，则会创建多个文件，并且 file 必须是一个字符标量，其中包含文件的基本名称，不带扩展名。（但它可以包含文件的路径。）

另请参见下面的详细信息。

project.file

逻辑标量，是否创建包含所有数据的单个 Pajek 项目文件，或者为每个项目创建单独的文件。请参阅下面的详细信息。

值

cohesive_blocks() 返回一个 cohesiveBlocks 对象。

blocks() 返回一个数字向量列表，其中包含顶点 ID。

graphs_from_cohesive_blocks() 返回一个 igraph 图列表，对应于内聚块。

cohesion() 返回一个数值向量，即每个块的内聚度。

hierarchy() 返回一个 igraph 图，表示内聚块的层次结构。

parent() 返回一个数值向量，给出块层次结构中每个内聚块的父块。层次结构根部的块没有父块，并为其返回 0。

plot_hierarchy()、plot() 和 export_pajek() 返回 NULL，不可见。

max_cohesion() 返回一个数值向量，每个顶点一个条目，给出其最内聚块的内聚度。

print() 和 summary() 返回 cohesiveBlocks 对象本身，不可见。

length 返回一个数值标量，即块的数量。

详细信息

内聚块是一种基于图顶点的结构内聚性（或顶点连通性）确定图顶点层次子集的方法。对于给定的图 \(G\)，如果 \(S\) 没有顶点连通性大于或等于 \(k\) 的超集，则其顶点子集 \(S\subset V(G)\) 被称为最大 \(k\) 内聚。内聚块是一个过程，通过该过程，给定一个 \(k\) 内聚顶点集，递归地识别最大 \(l\) 内聚子集，其中 \(l>k\)。因此，找到一个顶点子集的层次结构，整个图 \(G\) 位于其根部。

函数 cohesive_blocks() 实现内聚块。它返回一个 cohesiveBlocks 对象。cohesiveBlocks 应被视为不透明类，即不应直接访问其内部结构，而是通过此处列出的函数。

函数 length 可用于 cohesiveBlocks 对象，它给出块的数量。

函数 blocks() 返回存储在 cohesiveBlocks 对象中的实际块。它们以数字向量列表的形式返回，每个向量包含顶点 ID。

函数 graphs_from_cohesive_blocks() 类似，但将块作为输入图的（导出）子图返回。各种（图、顶点和边）属性都保存在子图中。

函数 cohesion() 返回一个数字向量，即不同块的内聚度。块的顺序与 blocks() 和 graphs_from_cohesive_blocks() 函数相同。

可以使用 hierarchy() 函数查询块层次结构。它返回一个 igraph 图，其顶点 ID 根据 blocks() 和 graphs_from_cohesive_blocks()、cohesion() 等函数中块的顺序排序。

parent() 给出每个块在其块层次结构中的父顶点，对于根顶点，它给出 0。

plot_hierarchy() 通过调用 igraph.plot 在活动的图形设备上绘制内聚块的层次结构树。

export_pajek() 函数可用于以 Pajek 格式导出图及其内聚块。它可以导出包含所有信息的单个 Pajek 项目文件，也可以导出一组文件，具体取决于其 project.file 参数。如果 project.file 为 TRUE，则以下信息将写入 file 参数中给出的文件（或连接）：(1) 输入图及其属性，有关详细信息，请参阅 write_graph()；(2) 层次结构图；(3) 每个内聚块一个二元分区。如果 project.file 为 FALSE，则 file 参数必须是字符标量，并用作生成文件的基本名称。如果 file 为“basename”，则会创建以下文件：(1) 原始图的“basename.net”；(2) 层次结构图的“basename_hierarchy.net”；(3) 每个内聚块的“basename_block_x.net”，其中“x”是块的编号，从一开始。

max_cohesion() 返回每个顶点的最大内聚度，即顶点最内聚块的内聚度。

泛型函数 summary() 可用于 cohesiveBlocks 对象，它会将一行摘要打印到终端。

泛型函数 print() 也定义在 cohesiveBlocks 对象上，如果在键入 cohesiveBlocks 对象的名称时会自动调用它。它会生成如下输出

 Cohesive block structure:
B-1 c 1, n 23
'- B-2 c 2, n 14 oooooooo.. .o......oo ooo
'- B-4 c 5, n  7 ooooooo... .......... ...
'- B-3 c 2, n 10 ......o.oo o.oooooo.. ...
'- B-5 c 3, n  4 ......o.oo o......... ...

左侧部分显示块结构，在本例中为五个块。第一个块始终对应于整个图，即使其内聚度为零。然后显示块的内聚度和块中顶点的数量。仅当显示足够宽时才会打印最后一部分，并按顶点 ID 显示块中的顶点。“o”表示包含顶点，点表示不包含顶点，并且顶点以十个为一组显示。

泛型函数 plot() 绘制图，显示其中的一个或多个内聚块。

参考文献

J. Moody 和 D. R. White。Structural cohesion and embeddedness: A hierarchical concept of social groups。American Sociological Review, 68(1):103–127, Feb 2003, doi:10.2307/3088904 。

参见

cohesion()

作者

Gabor Csardi csardi.gabor@gmail.com 用于当前实现，Peter McMahan (https://socialsciences.uchicago.edu/news/alumni-profile-peter-mcmahan-phd17-sociology) 在 R 中编写了第一个版本。

示例


## The graph from the Moody-White paper
mw <- graph_from_literal(
  1 - 2:3:4:5:6, 2 - 3:4:5:7, 3 - 4:6:7, 4 - 5:6:7,
  5 - 6:7:21, 6 - 7, 7 - 8:11:14:19, 8 - 9:11:14, 9 - 10,
  10 - 12:13, 11 - 12:14, 12 - 16, 13 - 16, 14 - 15, 15 - 16,
  17 - 18:19:20, 18 - 20:21, 19 - 20:22:23, 20 - 21,
  21 - 22:23, 22 - 23
)

mwBlocks <- cohesive_blocks(mw)

# Inspect block membership and cohesion
mwBlocks
#> Cohesive block structure:
#> B-1         c 1, n 23
#> '- B-2      c 2, n 14   oooooooo.. .o......oo ooo 
#>    '- B-4   c 5, n  7   ooooooo... .......... ... 
#> '- B-3      c 2, n 10   ......o.oo o.oooooo.. ... 
#>    '- B-5   c 3, n  4   ......o.oo o......... ... 
blocks(mwBlocks)
#> [[1]]
#> + 23/23 vertices, named, from b122831:
#>  [1] 1  2  3  4  5  6  7  21 8  11 14 19 9  10 12 13 16 15 17 18 20 22 23
#> 
#> [[2]]
#> + 14/23 vertices, named, from b122831:
#>  [1] 1  2  3  4  5  6  7  21 19 17 18 20 22 23
#> 
#> [[3]]
#> + 10/23 vertices, named, from b122831:
#>  [1] 7  8  11 14 9  10 12 13 16 15
#> 
#> [[4]]
#> + 7/23 vertices, named, from b122831:
#> [1] 1 2 3 4 5 6 7
#> 
#> [[5]]
#> + 4/23 vertices, named, from b122831:
#> [1] 7  8  11 14
#> 
cohesion(mwBlocks)
#> [1] 1 2 2 5 3

# Save results in a Pajek file
file <- tempfile(fileext = ".paj")
export_pajek(mwBlocks, mw, file = file)
if (!interactive()) {
  unlink(file)
}

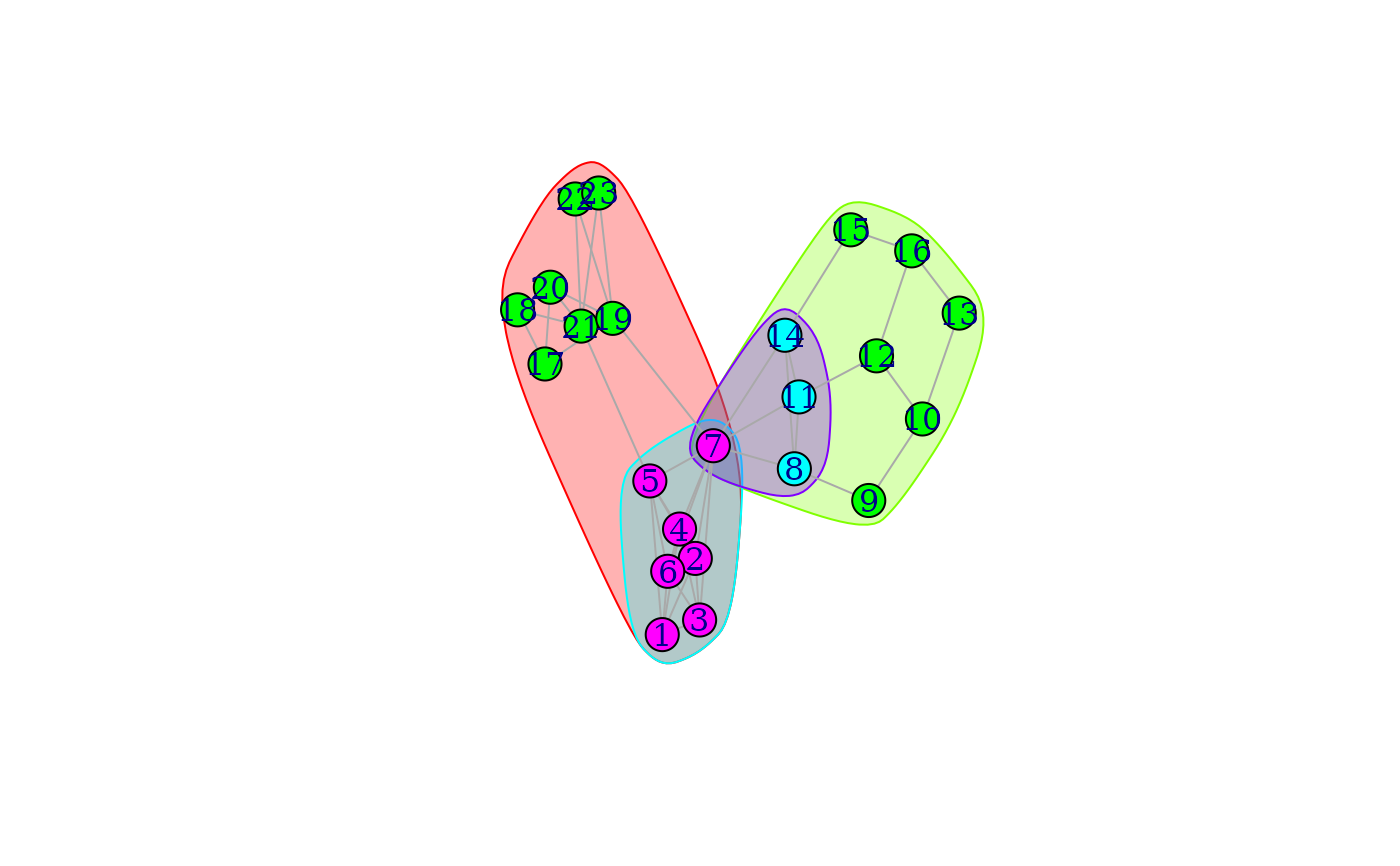
# Plot the results
plot(mwBlocks, mw)


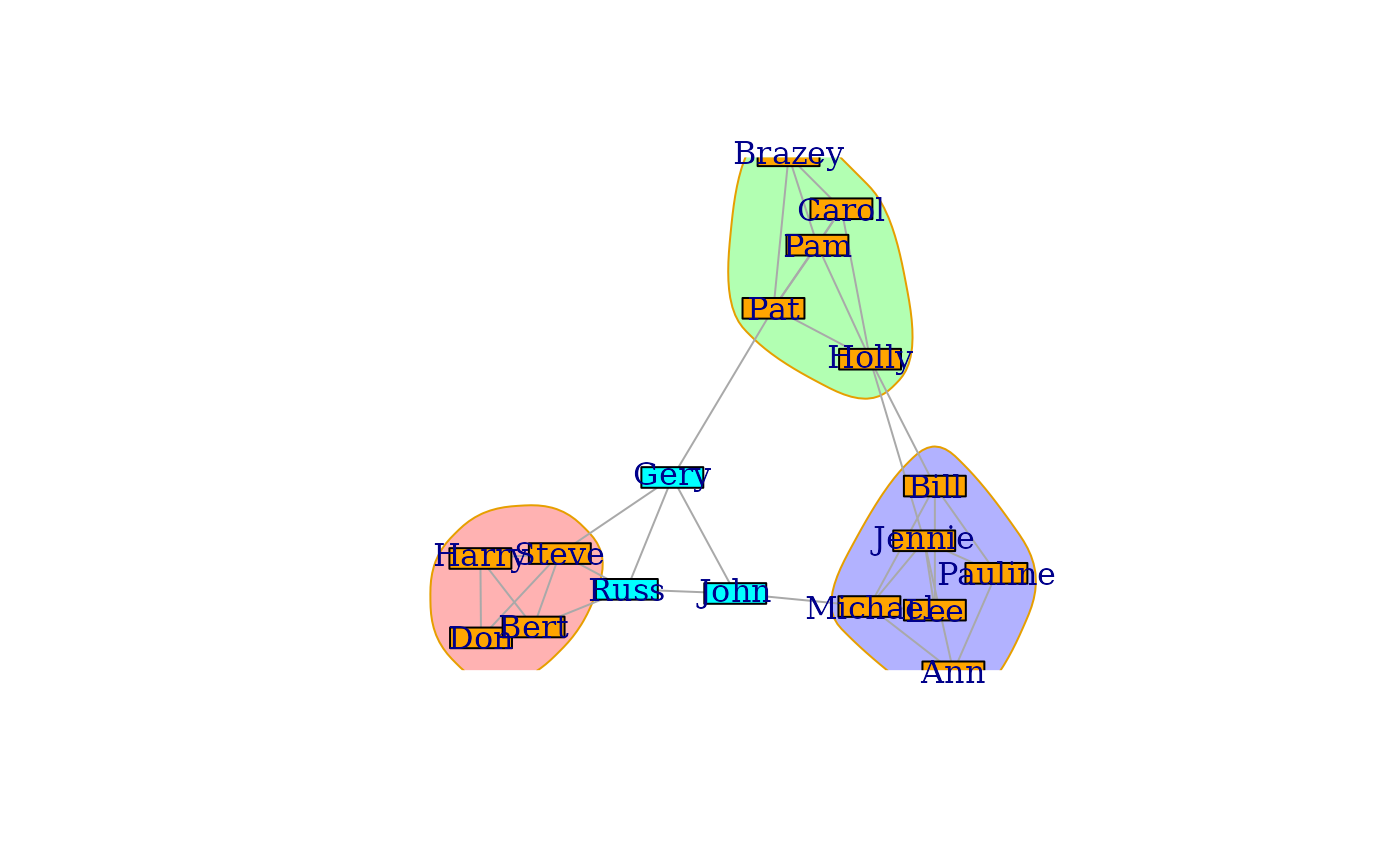
## The science camp network
camp <- graph_from_literal(
  Harry:Steve:Don:Bert - Harry:Steve:Don:Bert,
  Pam:Brazey:Carol:Pat - Pam:Brazey:Carol:Pat,
  Holly - Carol:Pat:Pam:Jennie:Bill,
  Bill - Pauline:Michael:Lee:Holly,
  Pauline - Bill:Jennie:Ann,
  Jennie - Holly:Michael:Lee:Ann:Pauline,
  Michael - Bill:Jennie:Ann:Lee:John,
  Ann - Michael:Jennie:Pauline,
  Lee - Michael:Bill:Jennie,
  Gery - Pat:Steve:Russ:John,
  Russ - Steve:Bert:Gery:John,
  John - Gery:Russ:Michael
)
campBlocks <- cohesive_blocks(camp)
campBlocks
#> Cohesive block structure:
#> B-1      c 2, n 18
#> '- B-2   c 3, n  4   oooo...... ........ 
#> '- B-3   c 3, n  5   ....ooooo. ........ 
#> '- B-4   c 3, n  6   .........o ooooo... 

plot(campBlocks, camp,
  vertex.label = V(camp)$name, margin = -0.2,
  vertex.shape = "rectangle", vertex.size = 24, vertex.size2 = 8,
  mark.border = 1, colbar = c(NA, NA, "cyan", "orange")
)