跳到内容

使用 Traag, van Eck & Waltman 的 Leiden 算法查找图的社群结构。

来源: R/community.R
cluster_leiden.Rd

Leiden 算法类似于 Louvain 算法 cluster_louvain()，但它速度更快，并且产生更高质量的解决方案。它可以优化模块度和 Constant Potts 模型，后者不受分辨率限制（请参阅预印本 http://arxiv.org/abs/1104.3083）。

用法

cluster_leiden(
  graph,
  objective_function = c("CPM", "modularity"),
  ...,
  weights = NULL,
  resolution = 1,
  resolution_parameter = deprecated(),
  beta = 0.01,
  initial_membership = NULL,
  n_iterations = 2,
  vertex_weights = NULL
)

参数

graph

输入图。它必须是无向图。

objective_function

是使用 Constant Potts 模型 (CPM) 还是模块度。必须是 "CPM" 或 "modularity"。

...

这些点用于未来的扩展，并且必须为空。

weights

边的权重。它必须是正数值向量、NULL 或 NA。如果它是 NULL 并且输入图具有“weight”边属性，那么将使用该属性。如果为 NULL 并且不存在此类属性，则边将具有相等的权重。如果图具有“weight”边属性，但您不想将其用于社群检测，请将其设置为 NA。对于此函数，较大的边权重意味着更强的连接。

resolution

要使用的分辨率参数。较高的分辨率会导致更多较小的社群，而较低的分辨率会导致较少较大的社群。

resolution_parameter

[Superseded] 请改用 resolution。

beta

影响 Leiden 算法中随机性的参数。这仅影响算法的细化步骤。

initial_membership

如果提供，Leiden 算法将尝试改进此提供的成员资格。如果没有提供参数，则算法只是从单例分区开始。

n_iterations

迭代 Leiden 算法的迭代次数。每次迭代都可以进一步改进分区。

vertex_weights

Leiden 算法中使用的顶点权重。如果未提供，则将根据 objective_function 自动确定。请参阅此函数的详细信息，了解如何解释顶点权重。

值

cluster_leiden() 返回一个 communities() 对象，请参阅 communities() 手册页以获取详细信息。

详细信息

Leiden 算法由三个阶段组成：（1）节点的局部移动，（2）分区的细化，以及（3）基于细化分区的网络聚合，使用非细化分区为聚合网络创建一个初始分区。在 Leiden 算法的局部移动过程中，只访问其邻域已更改的节点。通过从每个集群内的单例分区重新开始并逐步合并子集群来完成细化。聚合时，单个集群可能由多个节点表示（这些节点是在细化中识别的子集群）。

Leiden 算法提供了几个保证。Leiden 算法通常是迭代的：一次迭代的输出用作下一次迭代的输入。在每次迭代中，保证所有集群都是连接良好且分离良好的。在没有发生任何更改的迭代之后，保证所有节点和某些部分都在本地最佳分配。最后，渐近地，保证所有集群的所有子集都在本地最佳分配。有关更多详细信息，请参阅 Traag, Waltman & van Eck (2019)。

正在优化的目标函数是

$$\frac{1}{2m} \sum_{ij} (A_{ij} - \gamma n_i n_j)\delta(\sigma_i, \sigma_j)$$

其中 \(m\) 是总边权重，\(A_{ij}\) 是边 \((i, j)\) 的权重，\(\gamma\) 是所谓的分辨率参数，\(n_i\) 是节点 \(i\) 的节点权重，\(\sigma_i\) 是节点 \(i\) 的集群，如果且仅当 \(x = y\) 时，\(\delta(x, y) = 1\) ，否则为 \(0\)。通过设置 \(n_i = k_i\)，节点 \(i\) 的度数，并将 \(\gamma\) 除以 \(2m\)，您可以有效地获得模块度的表达式。

因此，当您将度数作为 vertex_weights 提供，并通过提供作为分辨率参数 \(\frac{1}{2m}\) 时，将优化标准模块度，其中 \(m\) 是边的数量。如果您没有指定任何 vertex_weights，则正确的顶点权重和 \(\gamma\) 的缩放将由 objective_function 参数自动确定。

参考文献

Traag, V. A., Waltman, L., & van Eck, N. J. (2019). 从 Louvain 到 Leiden：保证连接良好的社群。Scientific reports, 9(1), 5233. doi: 10.1038/s41598-019-41695-z, arXiv:1810.08473v3 [cs.SI]

参见

参见 communities() 以从结果中提取成员资格、模块化分数等。

其他社群检测算法：cluster_walktrap(), cluster_spinglass(), cluster_leading_eigen(), cluster_edge_betweenness(), cluster_fast_greedy(), cluster_label_prop() cluster_louvain() cluster_fluid_communities() cluster_infomap() cluster_optimal() cluster_walktrap()

社群检测 as_membership(), cluster_edge_betweenness(), cluster_fast_greedy(), cluster_fluid_communities(), cluster_infomap(), cluster_label_prop(), cluster_leading_eigen(), cluster_louvain(), cluster_optimal(), cluster_spinglass(), cluster_walktrap(), compare(), groups(), make_clusters(), membership(), modularity.igraph(), plot_dendrogram(), split_join_distance(), voronoi_cells()

作者

Vincent Traag

示例

g <- make_graph("Zachary")
# By default CPM is used
r <- quantile(strength(g))[2] / (gorder(g) - 1)
# Set seed for sake of reproducibility
set.seed(1)
ldc <- cluster_leiden(g, resolution = r)
print(ldc)
#> IGRAPH clustering leiden, groups: 2, mod: NA
#> + groups:
#>   $`1`
#>    [1]  1  2  3  4  5  6  7  8 10 11 12 13 14 17 18 20 22
#>   
#>   $`2`
#>    [1]  9 15 16 19 21 23 24 25 26 27 28 29 30 31 32 33 34
#>   
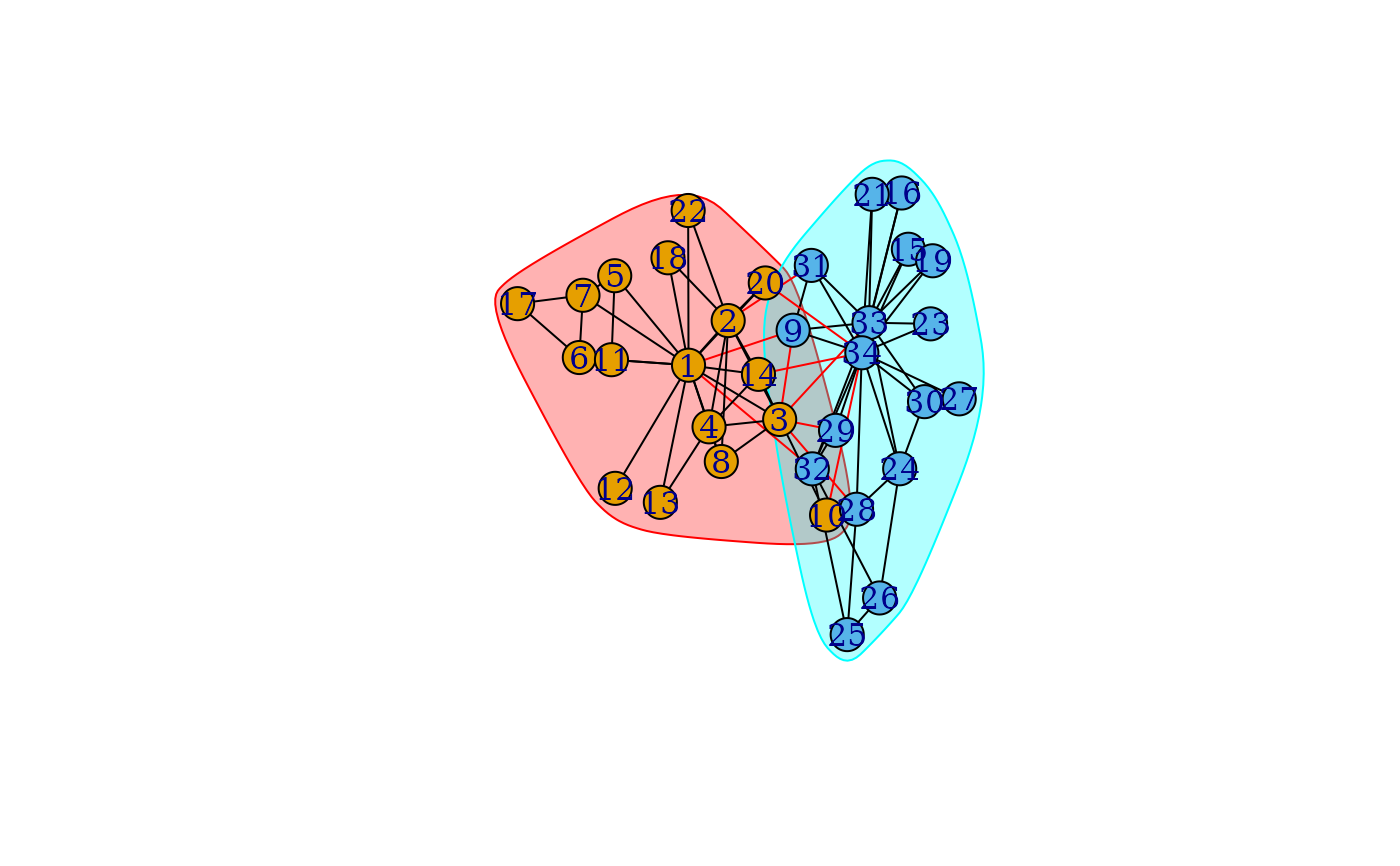
plot(ldc, g)