跳到内容

基于顶点适应度分数的随机图

来源: R/games.R
sample_fitness.Rd

此函数生成一个非增长的随机图，其边概率与节点适应度分数成正比。

用法

sample_fitness(
  no.of.edges,
  fitness.out,
  fitness.in = NULL,
  loops = FALSE,
  multiple = FALSE
)

参数

no.of.edges

生成的图中的边数。

fitness.out

一个数值向量，包含每个顶点的适应度。对于有向图，这指定了每个顶点的出度适应度。

fitness.in

如果NULL（默认值），则生成的图将是无向图。如果不是NULL，则它应该是一个数值向量，并且指定每个顶点的入度适应度。

如果此参数不是NULL，则生成有向图，否则生成无向图。

loops

逻辑标量，是否允许图中的环边。

multiple

逻辑标量，是否允许图中的多重边。

值

一个 igraph 图，有向或无向。

详细信息

此函数生成一个有向或无向的随机图，其中顶点 \(i\) 和 \(j\) 之间边的概率取决于所涉及的两个顶点的适应度分数。对于无向图，每个顶点都有一个适应度分数。对于有向图，每个顶点都有一个出度和一个入度适应度，并且从 \(i\) 到 \(j\) 的边的概率取决于顶点 \(i\) 的出度适应度和顶点 \(j\) 的入度适应度。

生成过程如下。我们从 \(N\) 个断开连接的节点开始（其中 \(N\) 由适应度向量的长度给出）。然后我们随机选择两个顶点 \(i\) 和 \(j\)，其概率与其适应度成正比。（当生成的图是有向图时，\(i\) 根据出度适应度选择，\(j\) 根据入度适应度选择）。如果顶点尚未连接（或者允许多重边），我们连接它们；否则，我们选择一个新的顶点对。重复此操作，直到创建所需数量的链接。

可以证明，每个顶点的期望度数将与其适应度成正比，尽管实际观察到的度数不会成正比。如果需要生成具有精确度序列的图，请考虑使用sample_degseq()。

此模型通常用于生成静态无标度网络。为此，您必须从所需的幂律分布中提取适应度分数。或者，您可以使用sample_fitness_pl()，它会为您生成具有给定指数的适应度。

参考文献

Goh K-I, Kahng B, Kim D: Universal behaviour of load distribution in scale-free networks. Phys Rev Lett 87(27):278701, 2001.

参见

随机图模型（函数）bipartite_gnm(), erdos.renyi.game(), sample_(), sample_bipartite(), sample_chung_lu(), sample_correlated_gnp(), sample_correlated_gnp_pair(), sample_degseq(), sample_dot_product(), sample_fitness_pl(), sample_forestfire(), sample_gnm(), sample_gnp(), sample_grg(), sample_growing(), sample_hierarchical_sbm(), sample_islands(), sample_k_regular(), sample_last_cit(), sample_pa(), sample_pa_age(), sample_pref(), sample_sbm(), sample_smallworld(), sample_traits_callaway(), sample_tree()

作者

Tamas Nepusz ntamas@gmail.com

static_fitness_game().

示例


N <- 10000
g <- sample_fitness(5 * N, sample((1:50)^-2, N, replace = TRUE))
degree_distribution(g)
#>   [1] 0.4612 0.2050 0.0834 0.0463 0.0264 0.0194 0.0138 0.0103 0.0083 0.0088
#>  [11] 0.0072 0.0057 0.0041 0.0037 0.0035 0.0031 0.0034 0.0027 0.0028 0.0016
#>  [21] 0.0023 0.0028 0.0011 0.0026 0.0017 0.0016 0.0009 0.0016 0.0016 0.0010
#>  [31] 0.0009 0.0011 0.0012 0.0010 0.0011 0.0010 0.0010 0.0014 0.0015 0.0012
#>  [41] 0.0022 0.0009 0.0011 0.0017 0.0011 0.0006 0.0004 0.0014 0.0003 0.0004
#>  [51] 0.0004 0.0003 0.0002 0.0000 0.0000 0.0000 0.0001 0.0000 0.0000 0.0000
#>  [61] 0.0000 0.0001 0.0000 0.0000 0.0000 0.0000 0.0000 0.0001 0.0002 0.0001
#>  [71] 0.0001 0.0002 0.0000 0.0000 0.0003 0.0006 0.0002 0.0005 0.0006 0.0007
#>  [81] 0.0013 0.0007 0.0011 0.0006 0.0008 0.0007 0.0007 0.0010 0.0016 0.0005
#>  [91] 0.0003 0.0012 0.0006 0.0010 0.0005 0.0006 0.0006 0.0007 0.0003 0.0002
#> [101] 0.0001 0.0000 0.0001 0.0003 0.0003 0.0001 0.0000 0.0000 0.0000 0.0001
#> [111] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
#> [121] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
#> [131] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
#> [141] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
#> [151] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
#> [161] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
#> [171] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
#> [181] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
#> [191] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
#> [201] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
#> [211] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
#> [221] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
#> [231] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
#> [241] 0.0000 0.0000 0.0000 0.0001 0.0000 0.0000 0.0000 0.0000 0.0000 0.0001
#> [251] 0.0001 0.0001 0.0002 0.0002 0.0001 0.0002 0.0003 0.0004 0.0003 0.0002
#> [261] 0.0000 0.0001 0.0004 0.0003 0.0002 0.0006 0.0008 0.0007 0.0005 0.0006
#> [271] 0.0004 0.0003 0.0009 0.0008 0.0008 0.0008 0.0005 0.0007 0.0004 0.0007
#> [281] 0.0008 0.0004 0.0008 0.0002 0.0002 0.0004 0.0005 0.0004 0.0010 0.0004
#> [291] 0.0000 0.0000 0.0003 0.0005 0.0001 0.0001 0.0003 0.0000 0.0000 0.0000
#> [301] 0.0001 0.0002 0.0000 0.0000 0.0001 0.0000 0.0000 0.0001 0.0002
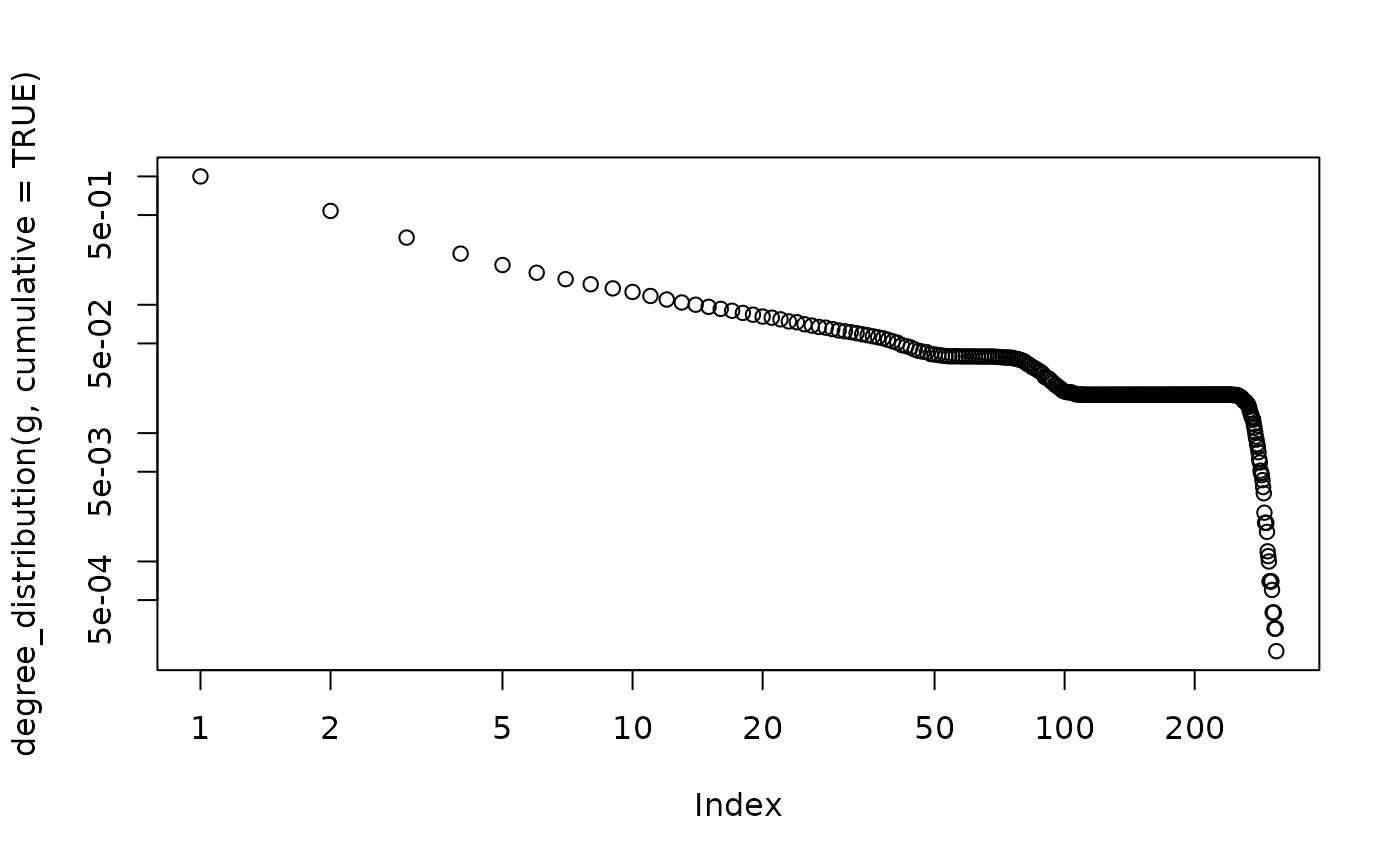
plot(degree_distribution(g, cumulative = TRUE), log = "xy")