跳到内容

基于顶点适应度分数的无尺度随机图

来源: R/games.R
sample_fitness_pl.Rd

此函数生成具有预期幂律度分布的非增长随机图。

用法

sample_fitness_pl(
  no.of.nodes,
  no.of.edges,
  exponent.out,
  exponent.in = -1,
  loops = FALSE,
  multiple = FALSE,
  finite.size.correction = TRUE
)

参数

no.of.nodes

生成的图中的顶点数。

no.of.edges

生成的图中的边数。

exponent.out

数值标量，度分布的幂律指数。对于有向图，这指定了出度分布的指数。它必须大于或等于 2。如果在此处传递 Inf，您将获得 Erdős-Rényi 随机网络。

exponent.in

数值标量。如果为负数，则生成的图将是无向图。如果大于或等于 2，则此参数指定入度分布的指数。如果为非负数但小于 2，则会生成错误。

loops

逻辑标量，是否允许在生成的图中出现环边。

multiple

逻辑标量，是否允许在生成的图中出现多重边。

finite.size.correction

逻辑标量，是否使用 Cho 等人提出的有限尺寸校正，请参阅下面的参考文献。

值

igraph 图，有向或无向。

详细信息

此游戏生成一个有向或无向随机图，其中顶点的度数遵循具有规定指数的幂律分布。对于有向图，可以分别指定入度和出度分布的指数。

该游戏只是使用 sample_fitness() 与适当构造的适应度向量。特别是，顶点 \(i\) 的适应度为 \(i^{-\alpha}\)，其中 \(\alpha = 1/(\gamma-1)\)，\(\gamma\) 是参数中给出的指数。

为了消除有向图情况下入度和出度之间的相关性，入度适应度向量将在设置后和调用 sample_fitness() 之前被打乱。

请注意，在游戏的原始公式中，对于小于 3 的指数，可能会观察到显着的有限尺寸效应。此函数提供了一个参数，允许您通过假设顶点 \(i\) 的适应度为 \((i+i_0-1)^{-\alpha}\) 来消除有限尺寸效应，其中 \(i_0\) 是一个适当选择的常数，以确保最大度数小于边数乘以平均度数的平方根；有关更多详细信息，请参见 Chung 和 Lu 以及 Cho 等人的论文。

参考文献

Goh K-I, Kahng B, Kim D: 无尺度网络中负载分布的普遍行为。Phys Rev Lett 87(27):278701, 2001。

Chung F 和 Lu L：具有给定度序列的随机图中的连通分量。Annals of Combinatorics 6, 125-145, 2002。

Cho YS, Kim JS, Park J, Kahng B, Kim D: Achlioptas 过程下无尺度网络中的渗流跃迁。Phys Rev Lett 103:135702, 2009。

参见

随机图模型（游戏） bipartite_gnm(), erdos.renyi.game(), sample_(), sample_bipartite(), sample_chung_lu(), sample_correlated_gnp(), sample_correlated_gnp_pair(), sample_degseq(), sample_dot_product(), sample_fitness(), sample_forestfire(), sample_gnm(), sample_gnp(), sample_grg(), sample_growing(), sample_hierarchical_sbm(), sample_islands(), sample_k_regular(), sample_last_cit(), sample_pa(), sample_pa_age(), sample_pref(), sample_sbm(), sample_smallworld(), sample_traits_callaway(), sample_tree()

作者

Tamas Nepusz ntamas@gmail.com

static_power_law_game().

示例


g <- sample_fitness_pl(10000, 30000, 2.2, 2.3)
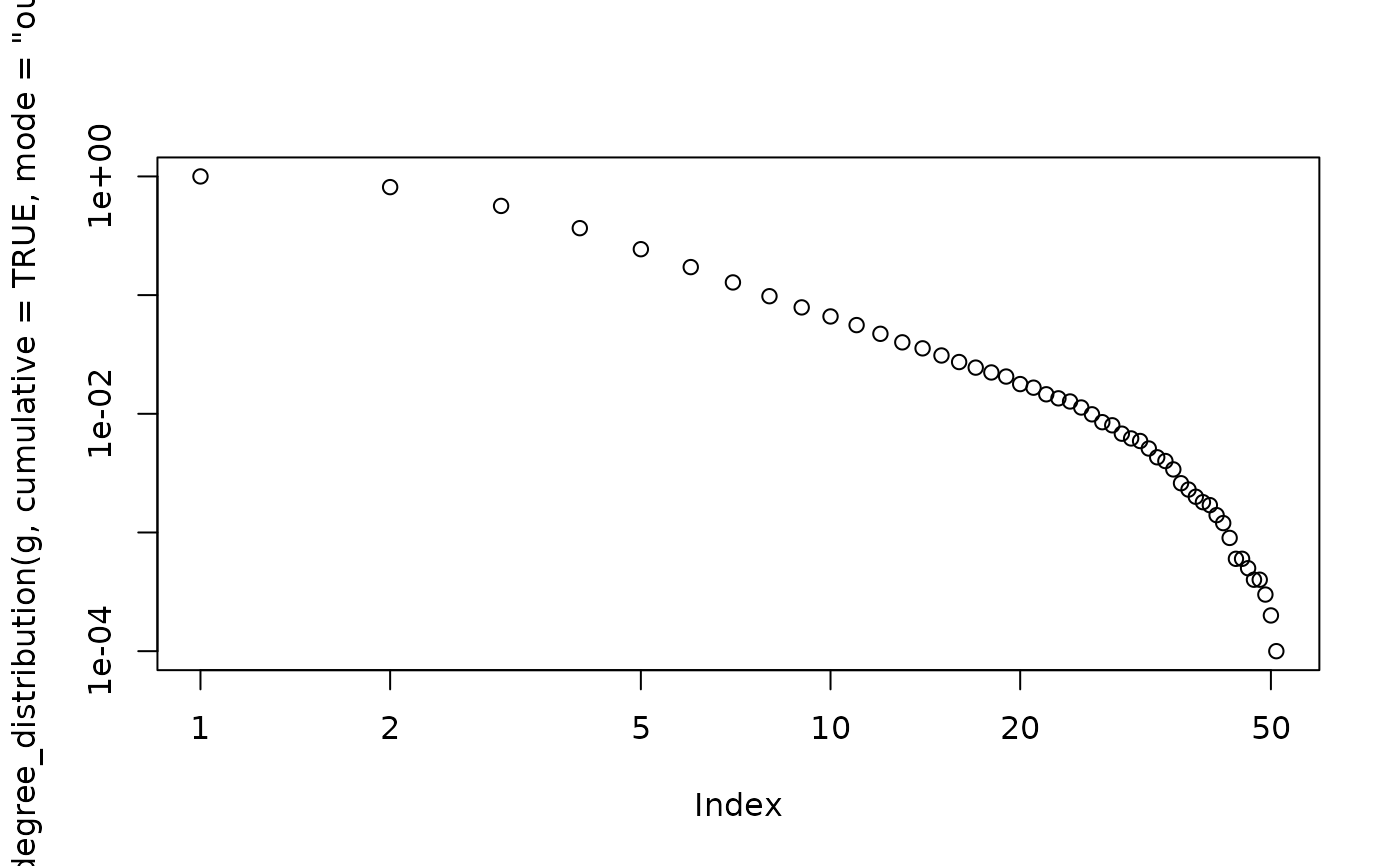
plot(degree_distribution(g, cumulative = TRUE, mode = "out"), log = "xy")